三等分角|从数理走向现实的展示

特有理

2021-10-1

三等分角是几何问题中，尺规作图的三大难题之一。这是个已被证明无法完成的任务。但是，同样还是用简单尺规，本人就可以用升维的方式和逼近的方式予以在实际中完成。完成的方法不是文章的重点，重点是展示数理与现实在自然中的联系通道；以及科学是如何辅助人类实现看似理论上无法达成的目标的。

升维法见下图：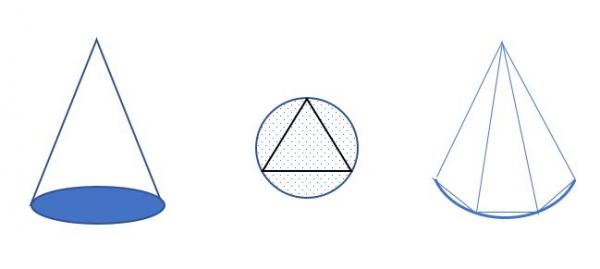

把二维的角平面卷曲成圆锥体，再用已经三等分的圆弧与锥体垂直接触。其中等边三角形的一个顶点位置对准锥面的接缝。标记好对应的另外两个顶点位置，将圆锥再展开到二维后就可以将角三等分。

逼近法参见最右侧的图示。追求的终极结果是得到三个等分的弧线或直线，方法根据不同的几何原理可以有很多种。不管一开始的线段如何离谱，只要采用误差对折的方式，误差减小的趋势将是2ⁿ形式。

两个重要的现实哲理：

1、 许多在低维度无解的问题，上升到高维度就可以解开。其哲理的本质在于，低维度的问题往往是高维度存在的低维度展开。许多被多数人认为无解的问题，其实是思考问题的人没有进入到更高的思维层次。哪怕一个二维圆形的一维投影确实是一条直线，且一维层次的人确实只看到了一个线段，但一维的事实并不是现实的全部。因此，任何理性的思维都应该给更高的维度留有余地。

2、 数理层面的“绝对不可能”在宇宙现实中只能是一个无穷远的非现实存在。事物之所以具有变化，宇宙之所以具有时间，就是因为宇宙是在用有限时间范围内的相对可能来逼近绝对不变的不可能。逼近的现实意义在于，绝对的正确是不存在的。以规尺作图的现实问题来说，规尺本身具有绝对存在的误差，线条的粗细也会产生必然的误差。理论意义的规尺和线条都是理想化的表达，而理想化的表达往往是可证的无法实现。然而，理论证明无法解决的问题，在现实层面是完全可以解决的。因为非理想化的逼近可以达到误差之内的相对理想，其代价就是逼近周期扩展所消耗的时间。这就是所谓格局与眼光的哲理本质。井底之蛙是空间的低格局和低视野；那么在时间维度中，同样也有井底之蛙的类似思维。

周末了，送给有能力思考的网友们解个闷儿。