勾股定理是初等數學中，一個比較重要的定理。其證明，有許多版本，比較流行的一種證明方法，如圖1，這是一個邊長分別為a,b,c的直角三角形，將四個完全相等的三角形，按照圖2所示的方式擺放，顯然，邊長為c的大正方形面積，為四個直角三角形的面積之和，再加上中間邊長為（b-a)的正方形面積，適當簡化，就得到勾股定理。

有關勾股定理的證明，有許多傳說。美國第x屆總統Jams, 有一個很聰明的證法，被傳為佳話。他將兩個完全相等的三角形如圖3擺放，虛線連接兩個頂點，顯然，梯形的面積，是三個直角三角形面積的和，寫出面積的表達式，稍作簡化，就得到勾股定理。

兩種方法都很直觀，有趣，巧妙，傳為佳話，理所當然。

不知你是否會想：美國總統，工作繁忙日理萬機，他所能解決的數學問題，能有多難呢？

這樣想就對了！請您看看表，對一下時間，參照前面的兩種證明方法，你一定可以在二十分鐘之內，自己再發現一種同樣直觀有趣巧妙的新方法。（證明自己有總統之才，事小；讓兒子孫子從中培養興趣自信志向，事大。本貼值咖啡一杯$0.99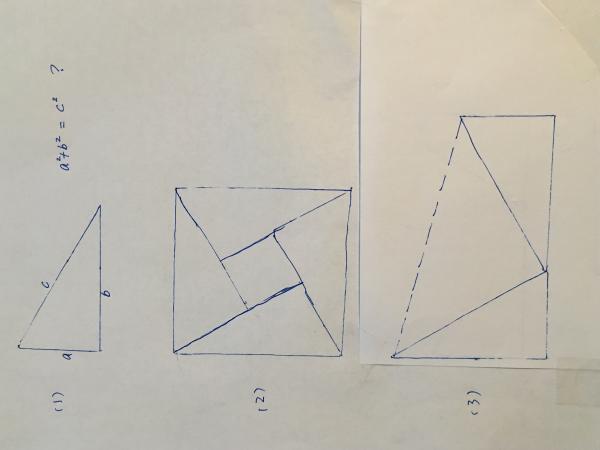）