你是典型的华人,认真工作,兢兢业业,辛苦工作多年,攒得一点儿薄财,勉强够你退休和你子女上学之用。 你的净资产(NW)为五十万美元. 拉斯维加斯赌场Mandalay Bay给你发来邀请,提供一个绝佳的博弈机会,让你发财。 赌场的博弈条件: 输赢概率50%,赔率令人乍舌: 押注: $0--$100--$10,000--$100,000----$500,000 赔率:$1--$110--$20,000--$1,000,000--$1trillion 你会作哪一种选择? 如果没有猜错的话,大部分人都会选择第一种赌法, 押注为$0,输了不赔,赢了赚1美元。赌徒或许会押$1万或$10万,赢了赚$2万或$100万,只有自杀倾向的人会选择把所有$50万家当都押注。 为什么会如此高的赔率不能吸引你下大注? 这里就是经济学上所谓的递减边际效用了 (diminishing marginal utility). 递减边际效益指人们获利到了一定程度,边际效用呈现出收敛-递减趋势。请看下图: 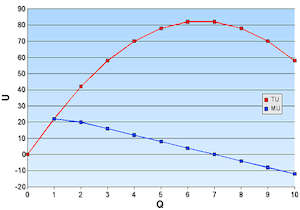
Q=获利, U=效用 这个图表直观的显示获利在7之前带来的效用是上升的,即每一份的获利所带来的快乐大于前一份的获利。可到了7之后,每一份获利带来的效用则成递减趋势,每一份获利带来的效用低于前一份获利。 回到最初的博弈问题,请看押$100赚$110策略,赚$110带来的边际效用为$100/$110=$91,小于损失的$100, 证明式:U(w+110)-U(w)≤U(w)-U(w-100) 。 在正常情况下,人们的避险趋向随着获利的增加而增强,如果你拒绝了 “$100/$110”的策略, 你就属于避险类型(risk-averse), 不会把全部家当五十万去赌一万亿的。因为$50万/$1trillion带给你的边际快乐微乎其微(5/10,000,000), 远远小于“$100/$110”的策略带给你的边际快乐。把以上浅显的逻辑用数学导数来阐述,就有了下面的定理: 已有财富 (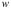 ), ), 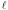 =损失, g=获利,财富效用 =损失, g=获利,财富效用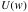 为严格增长,弱性收敛, 为严格增长,弱性收敛,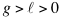 , , 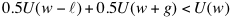 , , 设,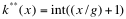 , ,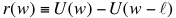 : : 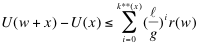
这个定理是柏克莱大学教授,著名经济学家Matthew Rabin 推导出来的投资风险分析的数学模式。推导过程可去阅读Rabin的原著 “Risk Aversion and Expected Utility Theory”. Rabin共推导出5种相似的数学模型, 本人觉得上面这一种模式与下面本人要阐述的人类社会避险趋向最为贴切, 故此引用。这个数学模式看上去深奥,其实所阐明的逻辑和上面的U(w +110) - U(w) ≤U(w) - U(w - 100)相同,人们有避险属性。 人类社会行为和人类经济行为的策略取值倾向是一致的,具有避险性。人们首先关注的是损失,其次才是获利。 只要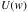 为增长, 人们就会选择他们认为成本最小的社会改革方案。 比如上面所说的 “押注为$0,赚$1”。这就是目前中国的现状, 大多数人的 为增长, 人们就会选择他们认为成本最小的社会改革方案。 比如上面所说的 “押注为$0,赚$1”。这就是目前中国的现状, 大多数人的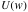 >0,利益集团不用说,七千万共党及其一亿三千万走狗(以每个共党一家三口计算),有房产有工作的城市居民,有地种,有买卖跑的农民等都是既得利益者,笃定的避险人群, 对于他们来说,不是社会有没有公义,需不需要改革的问题, 而是自己愿意为社会改革和进步所付的代价有多大的问题。如果把本文开头的赌博例子放在这里就能很形象的说明问题。 民主人士描绘的美好的西方民主自由法制就好象是赌场承诺的$100万或$1万亿的高回报。可为此社会将会付出什么样的代价是个未知数, 也就是所谓的不确定性(uncertainty). 这种不确定性恰恰是“投资者”所厌恶的,是无法量化的风险。 所以人们就会自然而然的选择避之,而选择无风险,或低风险的“循序渐进”的改良($0/$1策略),避开高风险高回报($50万/$1T策略)的孤注一掷。 其实这种抉择方式不仅仅是中国社会, 任何社会包括美国都是这样,社会的总体行为是避险,而不是趋险。 >0,利益集团不用说,七千万共党及其一亿三千万走狗(以每个共党一家三口计算),有房产有工作的城市居民,有地种,有买卖跑的农民等都是既得利益者,笃定的避险人群, 对于他们来说,不是社会有没有公义,需不需要改革的问题, 而是自己愿意为社会改革和进步所付的代价有多大的问题。如果把本文开头的赌博例子放在这里就能很形象的说明问题。 民主人士描绘的美好的西方民主自由法制就好象是赌场承诺的$100万或$1万亿的高回报。可为此社会将会付出什么样的代价是个未知数, 也就是所谓的不确定性(uncertainty). 这种不确定性恰恰是“投资者”所厌恶的,是无法量化的风险。 所以人们就会自然而然的选择避之,而选择无风险,或低风险的“循序渐进”的改良($0/$1策略),避开高风险高回报($50万/$1T策略)的孤注一掷。 其实这种抉择方式不仅仅是中国社会, 任何社会包括美国都是这样,社会的总体行为是避险,而不是趋险。 一定会有人问:既然人类有避险的属性, 那历史上的革命从何而来? 非常有意义的问题。有两种情况可能改变人们的避险趋向: 一是设最小风险<0, 二是提高输赢,特别是高回报的输赢概率。第一种情况让人民失去了避险的手段,不赌即输,失去已有的财富。回到上面的博弈例子,以“不押注赔$1”策略取代“押$0赚$1”策略,就会改变人们避险趋向;第二种情况则使孤注一掷变得垂手可得。如果把$50万/$1万亿的胜算概率提高到80%或更高,人群的趋险性就会增长。以上这两个条件只要出现其中之一或同时出现,就产生了革命的条件。 国民党失败的土地政策让农民绝望,不赌即输,才有了老毛的共党革命成功。这是第一种条件。最近的利比亚革命,由于北约参战,反对派胜算大增,原本迟疑的部落一边倒, 大家都尽早地卡位,以便在革命成功后取得最大利益回报,茉莉革命在利比亚成功,这是第二种情况。 看到这里,海外民主斗士,包括万维的几位民主博客应该会豁然开朗了,你们无法改变中国社会的最小风险值,但你们可以通过把美国和西方拉进中国的民主进程来,增加你们的胜算率。 这是你们成功的唯一途径,如果能让美国F-22和超级航母群来向中国输出民主, 胜算更大. | 