数学? 三分钟!(3)
上一则谈到了有关求解三次方程的恩恩怨怨,许多人对卡达诺不地道的做法持批评态度,故事有必要托展一下。卡尔达诺虽然坑蒙拐骗,但他的数学天赋与成就, 在人类的历史上,是屈指可数的。联想到他的生活背景, 对他的批评就不会太苛刻。 他的家庭生活是十分不幸的, 其长子因为杀害红杏出墙的太太而遭到处决, 他的小儿子是一个纨绔子弟,一再盗窃卡尔达诺的财产,卡尔达诺不得不一次又一次将他送进监狱。后来,卡尔达诺因为推算耶稣的生辰八字,被控大逆不道,可叹的是,他的儿子极力投入了对他的指控。 三次方程是数学发度史上的一个里程碑,自从卡尔达诺在其<<大书>>之中公布其解法之后, 五百多年来,三次方程的故事仍然是学者们津津乐道经久不衰的话题。 在中学生数学训练中, 三次方程的解法也可以作为很重要的一节, 一个优秀学生,如果在简单的提示下,自己推导出解法,是令人振奋的(笔者曾经辅导的学生,不少人有过很好的体验。参考资料The
Art of Problem solving中有提示) 。对于一般的同学来说,适当地了解与尝试,也很鼓舞士气。毕竟在解决三次方程之前,人类几千年的数学水平,也就是能求解部分二次方程。解三次方程,曾是人类智慧的高度,让孩子们尝试它,就已经接近了它! 故事终归是故事。家长们更关心的可能还是如何提高孩子的数学成绩,如何考出好的ACT,SAT分数;是否能找到学好数学的捷径与诀巧。相信数学学习中,捷径和诀巧是有的,初等数学毕竟是很成熟的学科,小学阶段要掌握的也就是加减乘除,中学阶段,依然还是加减乘除,是针对代数的加减乘除。上中学后, 许多孩子数学成绩差,症结就在代数式的四则运算不熟练,因式分解不到位 ,不理解因式分解的目的。只要加强这一部分的训练,很多小孩的成绩就会显著提高,很少有例外。 下面举一个例子,从中可以窥见数学的学习技巧。是一个与三角形有关的问题。
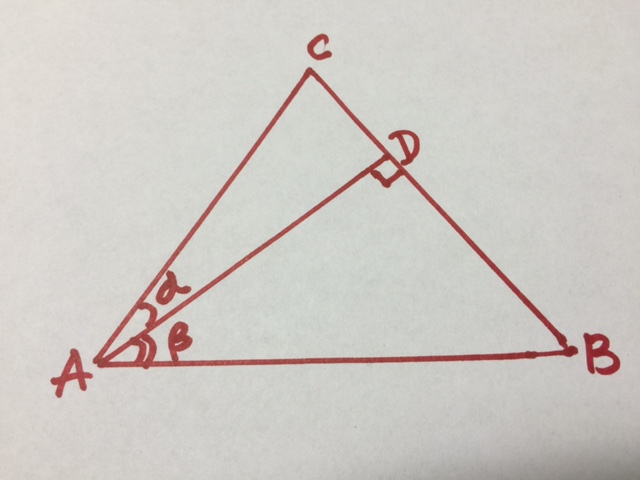
如图所示
: 有任意三角形ABC, AD是BC边上的高, AD的值为1, 由此可知: AC=1/ cos α, AB=1/ cos β,DC=tan α,
DB=tan β; 先回顾一下几个基本概念: 三角形的面积等于底乘高除2; 在直角三角形中,正弦是对边比斜边; 余弦是邻边比斜边; 正切是对边比邻边; sin α = cos(900- α); sin(- α)= - sin α; cos (- α)=cos α ; sin 2α +cos2 α =1。有了这些基本概念, 再来看问题: 很显然, 这个三角形的面积可以由大三角形ABC直接得到, 也可以由两个直角三角形ADC和 ADB相加而得, 其值相等, 即:
|
|
∆ABC
|
|
∆ADC +∆ADB
|
(1)
| |
|
|
|
|
| |
|
AB•AC sinA
|
|
AD•DC + AD•DB
|
(2)
| |
|
|
|
|
| |
|
|
|
tan β
|
(3)
| |
|
|
|
|
| |
|
|
|
|
(4)
| |
|
|
|
|
| |
|
sin(α+ β)=sin α cos β+cos α sin β
|
(5)
|
这就是三角学中的和角定理。 一般八九年级的孩子, 适当提示,都能重现推导过程 。如果再作一些简单变化, 如: 让β = α ,或者α=2* α /2 等等, 可进一步得到一系列的三角函数公式:
sin(α- β)= sin α cos β - cos α sin β;
sin(2α) = 2sin α cos α;
sin(α/2)= ;
cos(α+ β)= cos α cos β - sin α sin β;
cos(α- β)= cos α cos β + sin α sin β;
cos(2α) = cos2 α – sin2 α = 2cos2 α - 1 = 1- 2sin2 α;
cos(α/2)= ;
tan(α+ β)= sin(α+ β)/ cos(α+ β) = ( α+)/ α )
tan(2 α)= 2 tan α /(1-tan2 α) ;
………
没有复杂的运算, 也不需要特别的记忆, 从一个简单的三角形, 便可直观而简洁地导出三角函数的和角定理, 差角定理, 半角定理, 倍角定理…, 几乎可以从中梳理出三角函数的大半河山,美国ACT与SAT的考试,基本上不超过这一程度。(这个题目与大陆七八年全国统考数学试卷中的第五题极为相似, 原考题是: 已知一个三角形∆ABC的三个角成等差数列, tanAtanC = 2 +, 顶点C对边上的高为4+; 求该三角形的三条边与三个角。 此题对文科生为25分, 理科生为20分。相对于七八年的考题, 这里的这道题目相对简单, 但信息更丰富。)
相信不少人能从中看到数学学习的轻松与巧妙, 同时也会意识到学校教学中许多内客的冗长与不足,有些耗时数周甚至数月的内容, 对多数华裔孩子, 只是几个小时的训练而矣。不过,本系列不再交流数学技巧与具体问题,不希望因为强调技巧与捷径,宣宾夺主舍本求末, 忽视数学发展中的思想,从而糟蹋一门学问; 更不希望雷同的技巧雷同的方法雷同的思想雷同的价值观,坑害下一代。本系列的目的是循着数学发展的历史轨迹,探询数学是什么。(下集继续折腾)
|
