引力是由光速变化造成的

根据量子力学基本粒子最基本的运动方程是Klein-Gordon方程。假设光在空间位置r和时间t的速度为c(r,t)，是个可变量。并且，进一步假设在光速变化时，Klein-Gordon方程为：

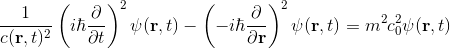
则可根据该方程推导出由光速变化造成的引力加速度为(详细推导请见参考该文献)：

g = -c(r,t)∇c(r,t)

或简写成：

g = -c∇c

这里g是引力加速度，∇c(r,t)是c(r,t)的梯度。也就是说，如有一物体在时间t时的位置为r，则其由光速变化造成的加速度为g，与其质量m无关。

如果只考虑物质造成的光速变化，忽略暗物质暗能量等其它可能造成的光速变化的因素，则光速变化与引力势Φ的关系是：

c = c0(1+Φ/c02)   

这里c0为标准光速，是个常数。该公式算出的引力红移与引力时钟变慢，符合实际观察。同时，该公式可以解释光线的引力弯曲。

引力势Φ可以通过解如下泊松方程获得:

∇2Φ = 4πGρ，

这里G是引力常数，ρ是质量密度。

利用引力势Φ，原引力场方程可以写成：

g = -(1+Φ/c02)∇Φ  = -(c/c0)∇Φ

在地球附近，引力势Φ不大，但是标准光速c0的值却很大。 所以Φ/c02非常小，可以忽略不计。这样就造成地球附近c≈c０。这时，引力场方程可以近似为：

g = -∇Φ   

而该方程便是著名的牛顿的引力场方程，牛顿的引力学得到了重建。而这里重建的条件是光速变化的假设及量子力学中的Klein-Gordon方程。

牛顿的引力场方程简单、易懂、和使用，已被无数的观测与实验所验证。由于该方程直接给出加速度，有了物体的加速度之后，便可直接得出该物体的运行轨迹。只是对于水星轨道，该引力方程计算出的结果与观测有非常小的偏差。

由于牛顿的引力方程是新的引力场方程在c≈c０情况下的近似。如果考虑到在太阳附近，由于太阳的质量是地球的300,000倍，引力势远远大于地球附近。而同时水星相对于其它行星离太阳最近，所以水星所在的位置的光速不再满足c≈c０。这时，若将牛顿引力方程g = -∇Φ 修正为新的引力学方程g = -(c/c0)∇Φ时，则原预测偏差可以得到修正。

所以，只要将牛顿引力方程做一个小小的修正，便可准确预测水星轨道近日点的进动。但是，当用广义相对论极为复杂与难懂的公式去修正偏差时，由于太过于复杂，就连爱因斯坦都需要当时世界上最优秀的数学家帮他计算水星轨道近日点进动。 另外，广义相对论太复杂，没法推算出行星的椭圆轨道。所以它只能在经典理论给出的椭圆轨道基础上，算出偏差。同时，广义相对论必须假设太阳是个质量均匀一个完全的球体。如不如此，或加入其它行星引力干扰，广义相对论复杂到没有人知道如何计算。