狭义相对论成立的条件是光速是不变的。但是，事实是地球表面不到半米高度变化，就可测到光速变化。另外，哈勃红移，所有星体附近的光透镜效果都说明光速变化是一普遍现象。光速不变只是个近似。在光速可变条件下，洛伦兹变换需要修正。

首先定义惯性系统为没有加速或旋转的系统。假设有两个惯性参考系s与s'，它们在时刻t=0时原点重合，且s'相对s以速度v沿x轴正方向运动。令一个事件在s系的坐标是(x,y,z,t)。其对应在s'系中的坐标为(x',y',z',t')。当光速不变时，(x,y,z,t)于(x',y',z',t')满足以下洛伦兹变换：

x'=γ(x-vt)

z'=z

t'=γ(t-vx/c²)

这里γ称为洛伦兹因子：

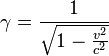
在光速可变条件下，设标准光速为c₀。在时刻t=0时，参考系s'的原点在参考系s的座标为x₀。在参考系s中参考系s'原点在时刻t为x₀+vt。设该点的光速为c(x₀+vt,t)。定义光速标准化因子α为：

α=c(x₀+vt,t)/c₀

修正后的洛伦兹变换为:

x'=γ(x-x₀-vt)

y'=y

z'=z

t'=αγ(t-v(x-x₀)/c²)

修正后的洛伦兹变换有如下特性：

1. 参考系s'的原点，光速永远是标准光速c₀。
2. 同时的相对性，Δt'=αγ(Δt-vΔx/c²)。当Δt=0,但Δx≠0, 则Δt'≠0。简单说参考系s同时不等同参考系s‘同时。
3. 长度收缩。参考系s静止的长度为Δx的尺子在参考系s'中为Δx'=Δx/γ。
4. 时间膨胀。参考系s静止的时钟走了为Δt时间，在参考系s'中为Δt'=αγΔt。
   
5. 速度相加。如有一物体在参考系s以速度u沿x轴正方向运动时，则该物体在参考系s'中的速度为u'=(u-v)/α(1-uv/c²).