前几天有一位叫做“海天”的博客就美国总统大选民意调查和预测写的一篇文章,介绍了美国民意调查和预测的一些做法,这篇文章还算客观,没有一些博客的“语不惊人誓不休”的光怪陆离。觉得这是个不错的话题,故在感恩节的轻松之余,就此也写一点自己的看法,纯粹是从技术角度讨论民调的准确性和前瞻性。 美国的民调五花八门,名目繁多,民调机构也是多如牛毛,全美的专业民调机构有近千家,调查方法和模型各不相同。不过原理却只有一个,即通过抽样来获取得人口的均值,根据统计学的原理,如果样品数量足够大而且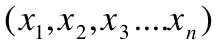 , 彼此独立,那样品均值等于实际均值(也称为母体均值-population mean): , 彼此独立,那样品均值等于实际均值(也称为母体均值-population mean): 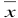 = μ , ( = μ , (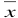 = 样品均值; μ=实际均值) 。这就是所谓的中心极限定理 (Central Limit Theorems), 这个定理指的是如果的均值μ 和方差σ2是有限的,只要样品数量n足够大,样本平均数的分布就趋于均值μ ,方差为σ2 / n的正态分布。如果把方差σ2 / n开方,就得到样品总量的标准差(standard deviation-σ): (m=样品均数),标准差是统计学里的一个基本但是却是应用广泛的一个概念,反映样品的离散程度,表示在正态分布中,样品均值落在母体均值正负两侧的概率。一个标准差代表了68.3%的样品均值会在( = 样品均值; μ=实际均值) 。这就是所谓的中心极限定理 (Central Limit Theorems), 这个定理指的是如果的均值μ 和方差σ2是有限的,只要样品数量n足够大,样本平均数的分布就趋于均值μ ,方差为σ2 / n的正态分布。如果把方差σ2 / n开方,就得到样品总量的标准差(standard deviation-σ): (m=样品均数),标准差是统计学里的一个基本但是却是应用广泛的一个概念,反映样品的离散程度,表示在正态分布中,样品均值落在母体均值正负两侧的概率。一个标准差代表了68.3%的样品均值会在(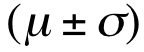 的范围之内,两个标准差指95.4%的样品值在 的范围之内,两个标准差指95.4%的样品值在 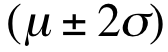 范围之内;三个标准差指99.7%的样品均值会落在 范围之内;三个标准差指99.7%的样品均值会落在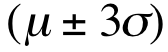 �范围之内。 这就是通常所说的“三个标准差规律”(68–95–99.7 rule)。下图标直观地反映了这个标准差规律: �范围之内。 这就是通常所说的“三个标准差规律”(68–95–99.7 rule)。下图标直观地反映了这个标准差规律:
�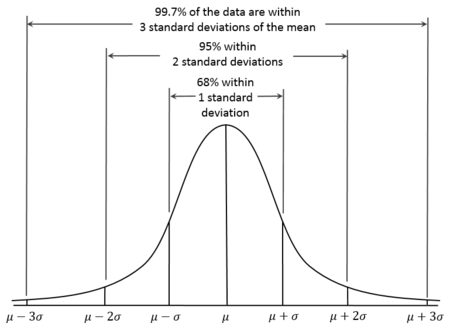 � �
与标准差相对应的百分比可以简单地看成统计上的置信度 (confidence level), 也就是我们平常说的“把握”,目前在政治经济人文等社会学科里通常采用的置信度是两个两个标准差,也就是95%的置信度,自然科学里的采用置信度要高于社会学科,一般在三个标准差。两个标准差的Z值 是1.96. 如果我们要求得两个标准差的样品误差范围(margin of error), 简单地把1.96放入标准差公式就可获得: 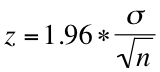
上面这些统计概念就是目前西方民调的基本原则。现在我们来回头看看川普和希拉里竞选总统时的民调和实际结果的差异。 下图是大选前的最后民调。(MoE=margin of error):
剔除没有样品数量和MoE的三家民调,根据上述的统计原则,我们获得9家民调的均值为 希拉里在全国民意上领先川普3.1%,MoE= 2.01%. 置信度为两个标准差 (95%)。 这就是说民调有95%的把握认为希拉里会以53.1% vs 46.9% (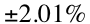 ) 的优势击败川普获得大选。让我们看看实际结果,到目前为止,在1亿2千万张的选票中,希拉里获得的票数超出川普200万张, 或者说1.7%。民调均值和实际民意均值接近,置信区间 (confidence interval)非常狭窄。 所以,这次民调并没有失误,川普获得大选是因为选举人体制的原因,而选举人体制在统计学上来说是加入了权重的因数,使得选票的分量因为地区的不同而发生了变化,可以这样说,“one people, one vote"在美国的政体下并不存在,不过这是政治话题,和这篇文章无关。 ) 的优势击败川普获得大选。让我们看看实际结果,到目前为止,在1亿2千万张的选票中,希拉里获得的票数超出川普200万张, 或者说1.7%。民调均值和实际民意均值接近,置信区间 (confidence interval)非常狭窄。 所以,这次民调并没有失误,川普获得大选是因为选举人体制的原因,而选举人体制在统计学上来说是加入了权重的因数,使得选票的分量因为地区的不同而发生了变化,可以这样说,“one people, one vote"在美国的政体下并不存在,不过这是政治话题,和这篇文章无关。
所以,所谓的取样误差是这次总统大选民调偏差的推测是没有意义的。现代的取样误差和美国早期的民调取样误差差不多,没有造成样品民意和实际民意的有统计意义上的区别。
那么,现在美国有没有可信度高的,建立在统计原理的民调预测模型? 很遗憾。 没有, 有不少民调机构在做预测,预测的统计模式不外乎通过回归把民意趋势线性化,
常见的模型有Mean absolute percentage error (MAPE), Mean squared deviation (MSD)和 Mean absolute deviation (MAD),我对于这些模型没有做过研究,只是知道原理而已,所以不在此讨论。建立在这些原理上的模式对于在误差范围之类的民调是无用的。我去“538”网站看过,读到538对于其他民调机构的预测准确性的评估,觉得很不靠谱。任何人都可以做到预测准确性的75%以上,方法很简单,只要民调差距超出误差范围3个百分点之上,就可以预测赢者,对于民调在误差范围之内的,可以随便猜,有50%的准确性。假设前后两种预测各占50%, 你就有75%的胜算。
上此在海天博客的回帖里,有一个女士大胆地用苍蝇落在候选人脸上作为败选的依据,你还别说,她的方法不比那个“538”的方法更不靠谱,反正都是瞎扯。
|
