2017 1 加密的算法有多种,从结构上看,只有两类:换位与替换,换位的经典体现为‘斯巴达密码棒’;替换则体现‘凯撒密码’,后续的发展几乎都在‘替换’的这种方式上,所有的加密算法都是在替换方式上的运算,恩格码机就是凯撒密码的物理实现。  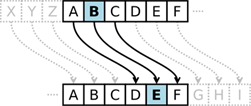 凯撒密码可以从结构上抽象为: En(X)=(X+n),mod(26),此后所有的密码算法都是其凯撒变种及演化,如每个字符采用不同的位移量n,因此而演化了密钥的算法,由密钥确定字符的位移量,人们探索的只是不同的算法F,字符集没有任何的改变。 这两类加密方式:换位与替换,在‘换位’思路上的密码进化似乎停止了,没有看到更多的进展。两类密码结构,两种不同的思路。 1941年11月22日,數學家艾德里安·艾伯特博士根據希爾的方法揭示出了所有替換式密碼的一個共同特點,那就是無論它們在設計細節上多麼的不同,其實質都對應著一組方程變換,正是這組變換決定了密碼系統的Sigma陣列。只要搞清一套密碼的方程體系,就能恢復出Sigma陣列,而這就等於實質上複製出了一台同樣的密碼機器。---引自《密码传奇,九》,古哥古点,附件1,这意味着,所有的替换算法都有机会被破解,也迫使的加密者寻求更为难以解破的密钥,如,两个大素数相乘,但是,本质依旧没有改变,因此,它们的风险依旧,一旦攻破算法,比如,找到加密算法中那两个足够大的质数,那么解密也就是顺理成章的事情了。 我注意到艾德里安·艾伯特博士所‘揭示出了所有替換式密碼的一個共同特點,那就是無論它們在設計細節上多麼的不同,其實質都對應著一組方程變換,正是這組變換決定了密碼系統的Sigma陣列’---艾伯特,这里,有一个前提,艾伯特并没有特别指出:‘运算在一个特定的、有限的字符集内’,所以,艾伯特应更为严紧地表达为:“特定的、有限的字符集内,替換式密碼的一個共同特點、、、、”。 从结构上看,这似乎是必然的,有限的字符集,有规律的、有限的运算一定会产生一个有限的结果,从哲学层面考虑‘凡存在,必有限’,剩下的只是如何揭示其有限了。 因此,打破加密过程中的‘有限性’是生成不可破解的密码的前提,这也正好验证了‘不重复的密码才是真正不可解破的密码’的经验陈述,因为,‘不重复’彻底打破了任何比对的可能性。 沿着斯巴达密码的思路,位移,以‘令人人都感到奇怪的是’短句在P1p2yyxx格式下编辑了一段密码: 00051314-00160402-00822011-16971504-00121903-00080801-01022012-01392103-00120301-00141910; 以p1yyp2xx格式下其编码为: 00130514-00041602-00208211-16159704-00191203-00080801-01200212-01213903-00031201-00191410; 其他的编码格式也可依次变换,读到这样一段数字串何人可解其意?在上面的短句中有‘人人’两个字,但是,它们的编码是不同的,在凯撒密码的算法中,这是不可能的因为凯撒运算En(X)=(X+n),mod(26),变换关系是一一对应的,是唯一的,因此,‘人’,或者‘Anyone’,经凯撒算法之后编码是唯一的,历史上的破解者也正是通过比对已经破解的密文与未解密文的代码从而找到编码规则的。 在使用中,两个数字之间的横线是不会有的,我在这里这样写,仅仅是为了阅读的方便。 我相信无人可解,即便他猜到了我的编码格式,除非他得到了我的密码蓝本《晚清七十年》的电子文本,该书共有498143个字符: 
由此文本,再依据编码结构,译出上面的数字串就非难事了,把它交给电脑,伸一个懒腰的时间,你的电脑就会让你读到译文。 假如我们把此算法从结构上做抽象,斯巴达算法对单一字符的运算可以表达为:En(X)=F(X, {Character Set}),对全文则等价为:Cipher=F(Paper,{Character Set}),有趣!看着眼熟吗?En(X)=(X+n),mod(26),它的逻辑表达式本质上与凯撒密码一样!所不同的是算法F与字符集(Character),因此,我们只需要把算法F定义为凯撒运算:En(X)与Dn(X),把字符集定义为英语的26个字母,则,斯巴达算法包涵了凯撒运算,甚至我们可以把凯撒运算作为斯巴达算法的特例。 斯巴达算法与凯撒运算具有相同的逻辑结构:Cipher=F(Character Set),凯撒运算在某个级别上的可重复性总是存在的,只是如何找到的问题,凯撒算法的风险来自与它封闭的字符集,‘凡存在,必有限’,而斯巴达算法的字符集是开放的,尽管运算(F)有限,但在开放的字符集上,它仍可以生成不重复,一次性的密码,使试图破解者无从下手,更无法试图以矩阵解读,因为它打碎了生成矩阵的前提:有限字符集。 因此,我的结论是,在凯撒算法思路上设计加密算法,F,在斯巴达算法的思路上,选择可变的,具有很大空间的开放字符集,由此生成具有更高可靠性的密文,並可以由此生成民用的,幾乎不可破解的通用加密算法。 在‘加密—解密’的博弈中最后的赢家是谁?我认为是加密方,加密与解密双方地位不对称,因为解密方很被动,加密方可以以很方便的手段更改运算法则,几乎不需耗费时间,而解密方则处于被动地位,一个算法,解密者需要耗费大量的时间,而且,加密方的算法几乎是无尽的。
|
