生日问题二

问题一：

在一次有50位客人的生日聚会上，出现至少有两人同一天生日（即同月同日，年不必相同）的概率是多少？

首先，当只有1个人时，概率为0%；当人数大于365时，根据鸽子笼原理，概率是100%。于是，在1到365这个区间内，我们直觉地认为，对应的概率是线性地从0％增长到100%。哪怕不线性，也不会陡峭得太离谱。所以对于50人来说，该概率应该在50/365，即七分之一左右。但事实上，这条曲线的增长劲头却是十分可怕。

图中p(n) = n个人中至少有两人同一天生日的概率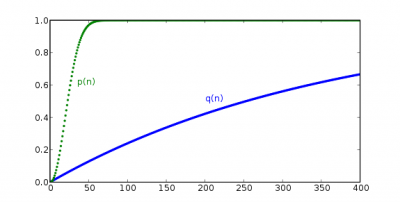

绿色的曲线，就是在不同的人数时，对应的存在相同生日的概率。它就像坐了直升机一样迅猛窜升，在50人时就已相当接近100%，与我们想象中的线性曲线有天壤之别。事实上，p(57) = 100%。如果把问题一，稍作改动，就能得到启发。

问题二：

在一次有50位客人（你是其中之一）的聚会上，至少有一人与你同一天生日（即同月同日，年不必相同）的概率有多大？

上图中q(n) = n个人（你是其中之一）里至少有一人和你同一天生日的概率。

同样地，我们把概率曲线描出来（即上图蓝色线），可以看到，它是十分平缓的。所以生日悖论的本质就是，随着集合里元素的增多，出现重复元素的概率会以惊人速度增长，而我们的直觉常常低估了它增长的速度。

独家原创，版权所有。未经作者同意，请勿转载。

参考文献：

[1] Paul Halmos. Wikipedia. http://en.wikipedia.org/wiki/Paul_Halmos

[2] Birthday Problem. Wikipedia. http://en.wikipedia.org/wiki/Birthday_Paradox

[3] M. Klamkin and D. Newman Extensions of the Birthday Surprise, Journal of Combinatorial Theory 3, 279–282. 1967

[4] D. Bloom. A Birthday Problem, American Mathematical Monthly 80, 1141–1142. 1973

[5] D. E. Knuth; The Art of Computer Programming. Vol. 3, Addison-Wesley, 1973

[6] Toobaz. Image. http://zh.wikipedia.org/wiki/File:Birthday_paradox.svg