凡事不可细究的物理学原理（一）

梦阮

圣人云，“水至清则无鱼，人至察则无徒”。

这其中的要义就是：凡事不可细究，不要走极端。大的方面还可以就行了。

在那个还没有量子力学的古代，先贤们能悟出此理，实属不易。

不论是自然世界也好，还是人类社会也罢，许多事情在大的方面，也就是宏观上，是有形的，可以观察和描述的。但如果你分的太细，纠缠在微小的细节之上，也就是在微观世界中，它们就会变得变幻莫测，让人捉摸不定。这正是量子力学中的海森堡测不准原理所阐述的内容：一个运动中粒子的位置，和它的动量不可以被同时确定。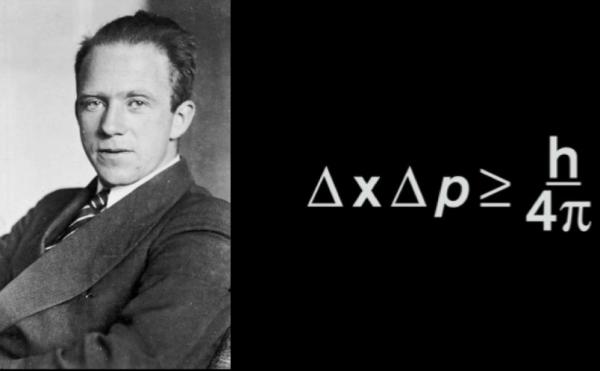

事实上，在由量子力学的奇怪规则支配的微观世界中，两个不同的观察者，可以对同一对象的行为做出相反而又都正确的记录。换句话说，微观世界事实本身实际上不是客观的，是主观的。观察者也是量子世界中强大的参与者。

根据量子力学，粒子可以同时处于多个位置或状态——被称为叠加态。但是奇怪的是，只有在没有观察到它们的情况下，叠加态才会存在。我们观察到一个量子系统，会迫使系统进入到确定的状态。量子的这一特性，已经在实验获得了多次证明，如著名的双缝实验。

著名的“薛定谔的猫”实验，说的也是"生死叠加"的微观思想。它是把微观领域的量子行为扩展到宏观世界的推演。这里必须要认识量子行为的一个现象：观测。微观物质有不同的存在形式，即粒子和波。通常，微观物质以波的叠加混沌态存在；一旦观测后，它们立刻选择成为粒子。

“薛定谔的猫”实验是这样的：在一个盒子里有一只猫，以及少量放射性物质。之后，有50%的概率放射性物质将会衰变并释放出毒气杀死这只猫；同时有50%的概率放射性物质不会衰变而猫将活下来。根据经典物理学，在盒子里必将发生“猫死”或“猫活”这两个结果之一，而外部观测者只有打开盒子才能知道里面的结果。在量子的世界里，当盒子处于关闭状态，整个系统则一直保持不确定性的波态，即猫处于既生且死，生死叠加的状态。猫到底是死是活必须在盒子打开后，外部观测者观测时，物质以粒子形式表现后才能确定。这项实验旨在论证量子力学对微观粒子世界超乎常理的认识和理解，可这使微观不确定原理变成了宏观不确定原理，客观规律不以人的意志为转移，猫既活又死违背了人们惯常的逻辑思维。

因此，该实验表明，至少对量子力学的局部模型来说，我们需要重新考虑客观性的概念。宏观世界中的事实似乎仍然是安全的，但是关于量子力学的现有解释如何能够容纳主观事实的问题，颇令人困惑。一些物理学家将新发展视为支持各自理论的线索，如平行宇宙的存在。其他人则将其视为“实体本质上依赖于观察者”理论的有力证据，例如量子贝叶斯主义，其中观察者的行为和经验是理论的核心关注点。

显然，这些都是关于现实和现象本质的深刻的哲学问题。这里的关键点，就是在于宏观和微观的差别。

比如，天空漂浮的云朵，远看时具有各式各样的形状。近看，则什么也没有。

佛家说的“万事皆空”，讲的就是这种微观世界里的“什么也没有”，什么也“无形”的要义。

以上全部说的是空间上的物体。

从时间的角度来讲，也是一样。历史就是由时间构成的。如果你站在宏观的时间角度去观察，则有重大的历史事件发生。如果你细分到一秒钟，一微秒，一毫秒，则历史上什么也没有发生。究其原因，就是因为，你分的太细了！

凡事，都赢在适度，毁在过度。情深不寿，慧极必伤。看开些，尽早！

独家原创，版权所有。未经作者同意，请勿转载。