凡事不可细究的物理学和数学原理(三) 梦阮 前文一(·测不准原理的爱情版本)侃了量子力学的测不准原理。 前文二(·凡事不可细究的物理学原理)(· 怪不得牛顿晚年去干这事儿)侃了物理学和数学的关系。 事实上,量子力学的测不准原理有其深刻的数学原理。今天洒家就义务给列位看官分解一二。 首先,海森伯格的测不准原理是说: 一个运动中粒子的位置,和它的动量,不可以被同时确定。若以Δx代表粒子位置的误差,Δp代表粒子动量的误差,则恒有 Δx·Δp ≥ h/4π 其中,h是普朗克常数。 从数学的角度来看,海森伯格的测不准原理可以表述为: 若以f(t)代表均值为零,方差为σ2的正态分布, 以Ff代表f的傅里叶变换。则Ff是一个均值为零,方差为1/σ2的正态分布。换句话说,D(Ff)·D(f) = 1。其中D代表方差。 一般而言,上述结论不可以推广到任意函数,因为并不是任意函数都可以是一个概率分布函数(p.d.f)。所谓p.d.f 函数,就是满足两个条件的函数: 1. f(x) ≥ 0 for all x: -∞ to ∞; 2. f(x) 从-∞到∞的积分等于1; 但是,根据著名的帕塞瓦尔定理(或称帕塞瓦尔等式,Plancherel Theorem)傅里叶变换F是一个幺正算符。也就是说,F算子保持函数的平方的积分为一性。 首先,一个p.d.f函数一定只取正值。任意函数f的平方f2就只取正值。如果f2是p.d.f, 则根据上面的帕塞瓦尔定理,Ff2就必为p.d.f. 因此,由上面的傅里叶变换等式就可以推出: D((Ff)2) D(f2) ≥ 1/2. 众所周知,在量子力学里,位置和动量互为“共轭变量”(conjugate variables)。因此, 它们的振幅概率函数,f2和Ff2,之间的关系正是傅里叶变换的关系。基于物理单位的换算,这其中仅仅相差也一个常量倍数: h/2π, h是普朗克常数。 所以,把方差D(f2) 换成Δx,把方差D((Ff2)) 换成Δp,再加上常量倍数 h/2π,我们就得到海森伯格的测不准原理不等式: D((F2)) D(f2) = Δx·Δp ≥ h/4π = 1/2 · h/2π 附录 傅里叶变换定理: 设f(t)为一个绝对可积的偶函数(i.e. f(t) = f(-t) for all t),则 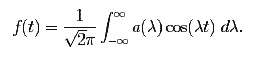
其中 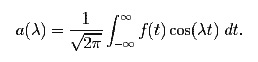
独家原创,版权所有。未经作者同意,请勿转载。
|
