在落體這個問題上,也有人為亞里士多德辯護(Rovelli , 2005)。亞里士多德考察的運動都是在流體中的運動,這是我們日常生活中唯一的可見的運動方式,即運動要麼在空氣中,要麼在水中。根據牛頓力學可以推導出球體下落時要達到一個恆定的速度,叫做終端速度。很容易推倒出終端速度隨重量的增加而增加。Rovelli認為物體通常會在很短的時間裡到達終端速度,人的感覺不可能分辨落體運動剛剛開始後的短暫時間內的速度變化,所以亞里士多德的速度應該是終端速度。這樣說來,亞里士多德的理論就成了牛頓力學在流體中的應用,或者說,牛頓力學整合了亞里士多德的理論。 我計算了保齡球,高爾夫球,冰雹和乒乓球在空氣中的自由落體(圖1)。隨着時間的增加,球體下落速度逐漸穩定。但保齡球則需要很長時間。如果我們將球舉過頭頂,同時投下,在1秒鐘之前幾個球都已經落地(圖2),這時我們的感官很難區分落體速度的差別。 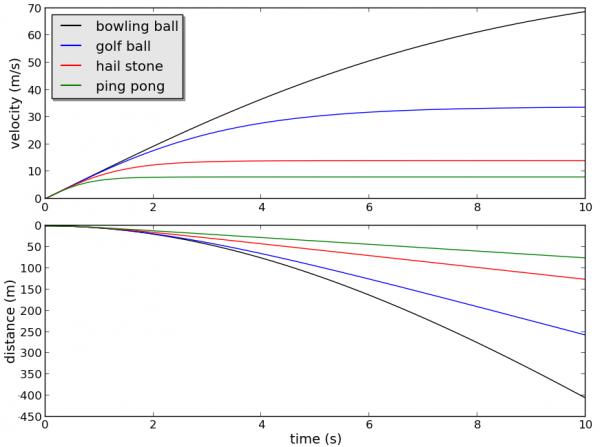
圖1. 保齡球,高爾夫球,冰雹和乒乓球在空氣中的自由落體。上邊的曲線圖為速度曲線,下邊的曲線圖為距離曲線。兩者的橫坐標為時間。
因此,我倒是覺得亞里士多德在落體運動上的觀察是不完備的,描述是不清晰的。如果用石頭和羽毛進行驗證,亞里士多德應該是對的。如果用兩塊大小不同的石頭試試就會發現他是錯的。但是,假如亞里士多德站在一個上百米高的建築上扔下同樣兩塊石頭,亞里士多德又可能是對的(圖2)。我們看看伽利略是如何解決落體問題的。首先,伽利略明確區分了兩種相反的作用,他想知道在沒有空氣阻力時運動是什麼樣的。換句話說,他對單個因子更感興趣。只有對單個因子進行研究,才能真正達到對因果關係的理解。伽利略在水中研究了落體運動,發現輕的非流線型物體的下落慢。由此推斷,空氣要比水稀薄,更接近真空,但對極端輕的物體如羽毛的運動,還是會產生足夠大的影響的。其次,伽利略用斜面對落體運動進行了定量的研究。由於計時技術的限制,他只能對小角度進行研究。在研究了幾個小角度後,發現速度和時間的線性關係。這裡,斜面是落體實驗的一個模型系統,通過這個系統推斷垂直下落的速度是如何變化的。
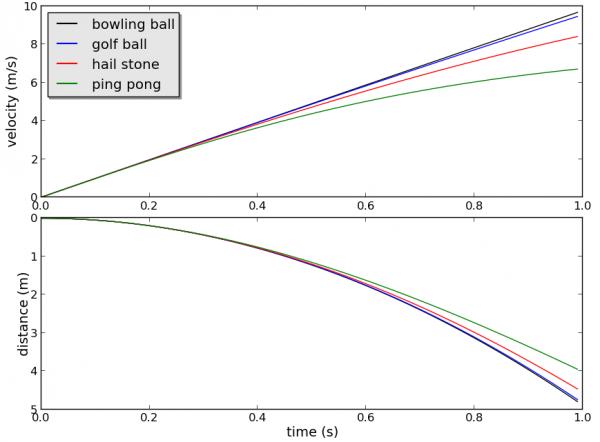
圖2. 圖1的局部放大。自由落體1秒後,四個不同落體到達地面的時間相差不大。在這個時間域裡,亞里士多德是錯誤的。 Philoponus之後,力學最主要的成就是法國牧師Buridan (1300-1361)和他的學生Oresme(1325-1382)建立的衝力理論。該理論認為運動是由物體本身的性質決定的,而不是外力。他將這一性質叫衝力。他認為拋射物從投擲者獲得衝力,衝力使拋射物運動。他認為衝力隨運動速度和物質的量而增加,衝力不會自發地消散,除非有空氣阻力或重力反抗衝力。只要衝力大於阻力,拋射物將保持運動並將無限地持續下去。這實際上已經非常接近現代的動量概念和動量守恆定律了。衝力理論被用來解釋天體運動。衝力理論為慣性概念的形成奠定了基礎。 經過Philoponus和後人修正後的運動學說是非常精緻的,很難用日常生活的經驗知識來證偽。亞里士多德的地心說,元素說和運動理論構成一個相對自洽的系統。否定其中的一個意味着否定或修正其它的觀點。例如,如果否定地心說,認為地球在轉動,空氣就應該落在後面而形成一股持久的東風。一塊石子向上拋去,就應該被地球的轉動拋在後面,而落在拋擲點的西面。人向西邊運動時會受到更大的阻力。另外,我們根本感覺不到地球的運動。為了回答這些問題,哥白尼在天體運行論中修訂了亞里士多德的觀點,認為當物體(元素)屬於整體時,也就是亞里士多德的自然位置,其自然運動是圓周運動。當元素離開整體時,如石頭離開地面,地上燃燒的火,這時的運動應該是兩個運動的合成,即直線運動和圓周運動。也就是說,儘管與自然位置分離,物體仍然分享地球的運動。因此,轉動的地球不會將空氣拋在後面而形成持久的東風。 這就是為什麼一直到哥白尼之後,人們才有機會重新審視亞里士多德的理論。如果以哥白尼的日心說取代地心說,同時保留亞里士多德的其它運動原理,就要補充新的假說以自圓其說,最後的結果將是一個具有無數補丁的理論。這樣的理論沒有意義,因為一個理論要用儘可能少的假說來解釋儘可能多得現象。這時需要的是一種的新理論。伽利略的慣性原理和相對性原理就是在這種情況下誕生的。 哥白尼之後,伽利略着手解決日心說和運動學說的矛盾。他的天文學理論和運動理論是緊密聯繫在一起的。伽利略觀察到金星相位變化,這是地心說難以解釋的,但用哥白尼日心說則很好解釋。他發現了土星的衛星,這意味着運動的土星不會將它的衛星拋在後面,因此,地球的運動也是可能的。然而,運動的地球需要新的關於運動的理論。為此,伽利略提出慣性定律,認為不受干預的物體會一直運動下去。伽利略提出了相對性原理,認為運動和靜止都是相對的,就像飄在海中的船,如果沒有顛簸,船中的人是感覺不到運動的。這意味着,如果太陽是宇宙的中心,人在高速運動的地球上和在勻速運動的船中是一樣的。月球不會被地球拋在後面。哥白尼的圓周自然運動不同於伽利略的慣性原理,前者是指元素在自然位置的圓周運動,就是地球的轉動。而慣性原理適用於任何勻速直線(地球表面)運動。
| 