《欣赏科学巅峰之光》

亲爱的朋友,前面曾经说过,
如果薛定谔方程是高中或大学课程, 我们的文章,就要从小学初级阶段说起, 您只要稍稍读一遍, 就会对这个世界顶级难题, 留下些或深或浅的印象的。 让我们先从薛定谔方程所依据的‘对应原理’说起。
量子力学可以在原有的经典物理中, 找到与自己相对应的规律。
所谓的对应原理是指在量子数很大的情况下, 量子理论所得结果, 应趋近以往经典物理学的结果,反之亦然。 薛定谔方程所对应的原理, 正是经典物理中的“能量守恒定律”。 让我们先看一下有关“能量守恒”的例子:

【图片说明】关于“势能”减小;“动能”增加的图示
在这个过程中,“势能”转化为“动能”。 看上图:这个处在下坡道的“骑车人”, 当他处在最高点时, 他具有一个由高度(h) 和质量(m)决定的势能; 当“骑车人”下坡时, 随着高度(h)的降低(即高度h值减少), 势能也在减小;但“能量守恒”, 是不允许能量由“有”而渐变为“无”的, 所以,在势能减少中, 另一种量,就产生并增加了, 这就是“动能”。 “动能”是由质量(m) 和速度(v)决定的。 在高点时,速度为0,动能也为0, 而随着“骑车人”高度的降低,速度就变大了, 这就意味着动能在不断地增大。 这种增加的动能,等于减少的势能, 所以,使得能量能保持守恒。 “骑车人”到达坡底时, 其势能抵达最小, 动能则达到最大。 如果此人有“胆”,或者他能像动画片那样, 在一瞬间将自己连同车子,全都化为一个圆球, 如同下面的彩图所示,

动能和势能
那么,这个“人和车”的组合, 就能上冲到与原来的高坡等高的点, 这种上冲之力, 就是一个与下坡相反的力, 但无论怎样, 其动能(K)与势能(V) 二者之和的总能(E)是不变的, 即, 总能E = 动能K+势能V 这个能量关系式, 同样适用于描述‘微观粒子’的运动, 只不过微观粒子的势能 不是由引力场引起的, 而是由微观粒子的势场引起的。 法国王子德布罗意(1892-1987) 沿着能量守恒的思路来想, 经过推演,得出了 ‘动量’与‘波长’关系式(波长 λ= h / 动量p); 薛定谔(1887-1961)在德布罗意的基础上 利用数学技巧经过繁复地步骤, 推出了微观粒子的‘波动方程’ (世称‘薛定谔波动方程’)。
“薛定谔方程(含时的)
是描述物理系统随时间演化的方程。
在三维空间里,
弥散于某处的微观粒子,
其“计算方程(含时的)”
可以具体地表现为:
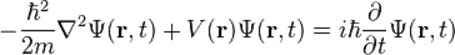

薛定谔方程中的符号及其含义,如下:
m 是质量;
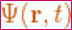
是‘位置 r和时间 t’的波函数;
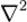
是某种计算符号,它代表的是有关‘微分’的计算。
“ψ” ,近似音,读作“普赛”, ‘普赛’代表波函数 。 “h”是普朗克常数;
“E”是所测粒子系统的总能量;
“ V”是势能。
“I”是虚数
虚数可以指不实的数字或并非表明具体数量的数字。 虚数的定义:平方是负数或根号内是负数的数。 注意:
公式中内含的‘总能’
及其所包含的‘动能’和‘势能’,
均表达了能量守恒的意义。
未完待续。谢谢阅读。
|
