19分钟,谢谢(建议打开全屏,以看清文字)。

《 红色和蓝色宇宙人的故事 2 》
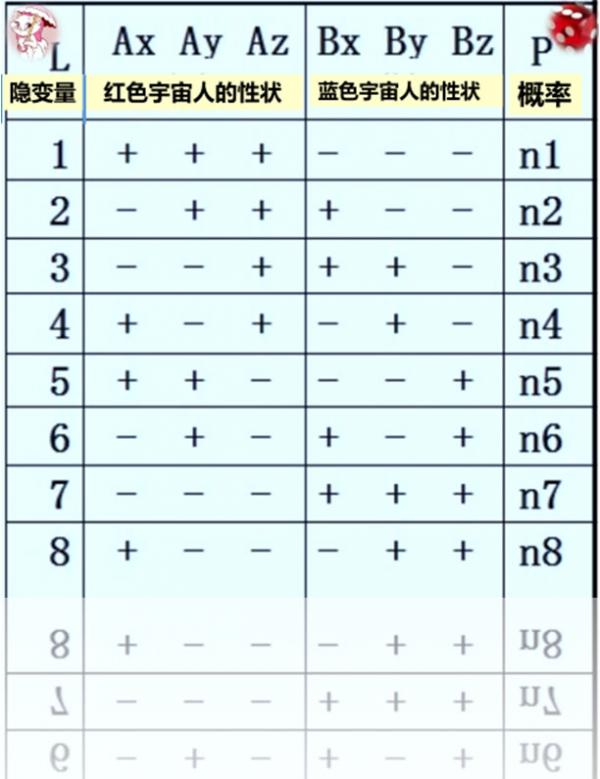
现在,我们有了一个概率观测《总表》,
就像古语所说“一念不生全体现”。 但是实际上我们并没有‘一时顿现’的能力, 我们还得按常规一点点来推演:
上表每一行都表示某种可能出现的情况, 例如,
[PDF] 第一横行左边 3 个格儿表示 我  观察到红色宇宙人 观察到红色宇宙人
在性别、高矮或眼睛的颜色(x,y,z)
这三个方面的性状都是“+”; 而第一横行右边的3格儿表示
你 
观察到蓝色宇宙人
在 3 种性状 (x、y 和 z )上,相应地均为“-”。 这种结果出现的可能性设为:N 1。 好吧,就让我们以这种原则
来类推表中的
第2 横行、第3 横行……直至第8 横行, 这种类推是小朋友都会做的事, 可是我们却很少有这样的耐性, 话说回来,如果每推一步都可以得100美金 或许我们都会‘趋之若骛’吧(骛wù,鸭)。 说到本人,由于要写博文,不得不吃尽苦头, 硬着头皮一直推下来。推的结果您猜怎样? 推的结果就是得出了 上面那个《概率观测总表》。 但是,推这个《表》光有吃苦精神还不行,顺利的推导, 还需要了解一些推导原则, 即:需要了解什么是概率的‘加法和减法’。 听到此有人会说,别逗了, 你以为我不知道什么是加法、减法吗? 当然您懂。但是这里要说的, 不是您以为的那种加、减法,这里要说的是 概率上的‘加法’和‘减法’。
(9)概率上的加法符号和减法符号 下面就让我们运用一些基础知识, 来进行概率上有关“相关性”的运算。
这里需要抛开所谓正号或负号概念, 概率上的 加法 和 减法 运算, 可做如下理解: 当在一种性状X(男女性别)来看时 A为+,而B同时为-, 或者 A不为+,而B不为-时, 如果这样, 它们就符合对(A x+,B x -)合作态度的规定, 于是就表示可以在《总表》相关之处 (即在相关符号前面), 写上  加号(+)。 加号(+)。 这里的“加号”不是“正号”的意思。 相反,如果在x性状上 A为+,而B也为+, 或者A为-,而B也为-
【就好像2个孩子在抢一个熊玩具, 你要这个熊,我也要这个熊), 那么这是对(Ax+,Bx-)组合的一种破坏
像是对‘和谐’的破坏;就好像2018年10月 美国国务卿冷冷地去了北京, 而北京官方亦冷冷地接待一样,双方不合作】,
这时我们就需要写上  减号(-)来表示相应的不合作概率。
(加减号要写在相关符号的前面) 。 这里的符号(-)是“减号”,不是“负数”。
(10) 在某种‘联合概率’中
‘加减法规则’不变!
首先看看什么是‘联合意义的概率’, 这里我们举例说明:如果
红色宇宙人 A,
在‘性别’上为男性时,即 x 为+ 时,
而蓝色宇宙人 B,
在‘高矮’上为‘高’时,即 Y 为+时
这 2 种观测结果的相关性是多少呢? 现在是2种完全 2不同的性状 (一个是性别X;一个是高矮Y), 这样的运算可以称为 联合意义的概率运算。 联合概率的加减法, 仍与前面所说的加减规则一样: 要是有一种观测, 符合(Ax)为+,以及(By)为+, 或者 ( Ax)不为+,以及(By)也不为+时, 我们就写上“加号”, 反之就写上“减号”。
未完待续,
感恩您的阅读!
|
