(2)用故事来说明“伽利略变换式”
为了熟知“伽利略变换式”, 需要读一下那篇妙趣横生的名著 《聊聊狭义相对论》
(第133至134页PDF版。下面的引用只有文字上的少许改动,全部内容均来自原文): “话说当年有 4 条变换式
与‘伽利略相对性原理’相对应, 那么,这 4条 变换式是何方神圣? 它们又长什么样呢? 好,为了说明问题,我们找个助手, 哈哈,就找那只蹦蹦跳跳的龅牙兔吧!
现在,有个重要任务交给你啦 (假设“你”是个男孩, 并且“你”还有一个‘玩伴’龅牙兔)!
空间直角坐标系
来,抱起这个空间直角坐标系, 静静站在这里,放平一点,别倾斜了,非常好。
龅牙兔出场了! 它也扛了个‘空间直角坐标系’, 一开始,它以为你这里有萝卜吃, 于是就站在了和你极靠近的位置, 并且努力地使它的坐标轴跟你的相重合。 然而那小子天生站不定,患有‘多动症’, 没过一会儿,它就开始以速度u 向前匀速跑去。 (这时)还有只可爱的小蜘蛛在你(们)的坐标系 (oxy或o’x’y’卦限的某处) 结了个小窝,呼噜呼噜进入梦乡。
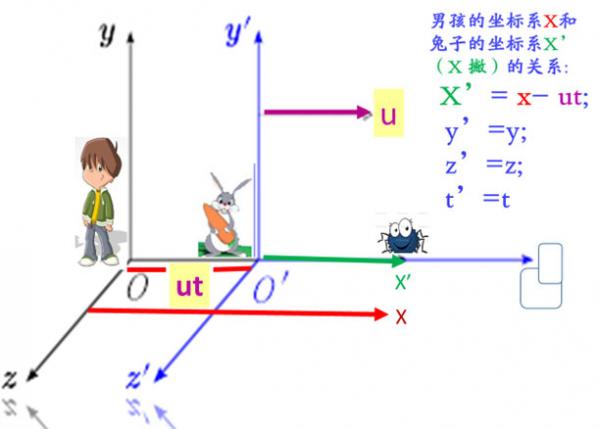
我们的目标是分别读出
蜘蛛小朋友在坐标系的坐标! 你很聪明,脱口而出:
“(在我这个静止的坐标系中的蜘蛛坐标是 (x,y,z),再让我看看表,现在的时间是t, 所以,蜘蛛的坐标是(x,y,z,t)!”
但是,要测那只兔子的就不那么容易了。 因为兔子的‘坐标系’在动, 搞了半天,兔子抢先弄出来。
“Oh Yeah!是(x’,y’,z’,t’) ! 我说伙计,你没我快吧! 嘿嘿,俺当年可是‘小兔幼儿园’的 数学第一啊!”
即使龅牙兔不张口,你也会以为它在说话, 那两只大门牙总是露在外面。
接下来,你和兔子吵了一整天,差点还揍了它, 终于,你胁迫它同意了 ‘你的坐标’跟‘它的坐标’之间的关系(在距离上)是:
X’= X - ut
因为在 t 时间里,兔子向前走了ut距离, 也就是离开你ut远了(本来你们是重合的), 所以你们的坐标原点应该相差了ut 那么大。 因此,就得到了上面的式子:
X’= X - ut
又因为你们的坐标系 在y轴和z轴的读数是相同的,
所以
y’=y z’=z
再有如果按照经典理论,认为 宇宙任何地方,时间都可以是一样的! 你的时间跟兔子的是一样的!
所以 t’=t
“那么,俺来总结一下……”
兔子摆出一副专家模样。
“我们的坐标关系是……”。
结论:
X’=X-ut(即距离在2个坐标系不一样)
Y’=Y (高度在2个坐标一样)
Z’=Z(宽度在2个坐标一样)
t’=t(时间在2个坐标相同) 这四个式子就是大名鼎鼎的伽利略变换式!
其实,也不过如此嘛, 连小学生都能推出来,对吧? 在数学上,当你根据伽利略变换式, 对牛顿定律进行变换时,会发现, 在你的坐标下的牛顿定律, 跟兔子坐标下的牛顿定律, 在形式上是完全相同的!
前面说过, 伽利略相对性原理说的是 “力学定律在任何惯性系中都是相同的”, 而相对性原理所对应的伽利略变化式 正好实现了这个目标。
谢谢阅读。
|
