《宇宙的灵魂、人命与广相论》

                  ——有厌恶、没有爱，即为入魔……

亲爱的朋友，

须知宇宙之所以生生不息、长久存在，

是因为宇宙有道。

道，即宇宙的生命。

道，是天地之魂（魂、灵体现在精神上）。

人，之所以能健康长寿，

是因为人——之所思、所想、所作、所为

——皆合天道。

合道之人、生命长久！

合道，就是一个人的灵魂（精神）

在天地舞台的全本演出。

天道是‘和谐’与‘仁爱’的同义词 ！

天道，即是日月的胸怀。

天地之道，即如山河般实实在在、

天地之道，即如大地般沉稳厚重……。

但是如今，我们看到，一些偏激之人，

对世俗是满满的厌恶、

这种厌恶大过仁爱。

而宇宙的本质、宗教的本质，正是仁爱 ！

有信仰的人，即便批判社会，

亦不离那份对众生的挚爱和关切。

如果只是指责厌恶，那是魔。

魔的行径，为主唾弃。

任何人不能打着基督的招牌，

反复、多次、全面、彻底地

发泄对中华民族、对中国文化的憎恶，

这种负面情绪的发泄，与天地不合、

且与主——背道而驰。

另外，还有些人，天天相互谩骂攻击，

互视对方为仇敌、

或者长期以来，持续地以对方为嘲讽对象，

搞得海外芸芸、不知所从、各派林立，

搞不好会形成一人一心（夸张了）。

一些人满怀情绪地发各种视频，

这些人上网，不是为清洗己心，

不是为忏悔以往的过错

（反正错在社会、错在别人）。

我们喜欢围观或喜欢挖别人的陋隐、

然后晒出来嘲讽打击，以示高洁——

最令人不解的是，

有人将政治斗争，（时不时地）变成黄色新闻，

打击女性毫不留情。

可能我们忘了——

人类对妇女儿童一直是保护的。

我们怎能容忍，

借故去伤害一位孩子的母亲。

还有些人沾沾自喜拥有海量从众——

殊不知群击数量高（在骂别人时），

或许只是为日后攒下海量的‘口业’而已。

试问朋友，一时枉得，能长久吗。还是少骂几句吧。

话说我们别别扭扭所学的相对论，

只是宇宙的物理定律，这物理定律

终究逃不脱精神的掌控。

学习广相论，

即是学习宇宙博大胸怀的一小部分。

学习，可以顺便陶冶、重组

或重新学习新的宇宙观和方法论。

从狭义角度、从物理角度说，

宇宙就是生活在许多公式定理之中的、

宇宙就是运化在许多术语概念之中的。

好，下面，让我们接着学习张天蓉的科普文章

（注：为适合更多人学习，编者添加一些图画，

           叙述文字也有些微改动）。

一分耕耘、一份收获。天道酬勤噢。

广义相对论之14

   ——什么是曲率和挠率？

朋友，前面说到，

罗氏几何（非欧几何之一）在当时看来很古怪，

罗氏几何得到古怪而不合常理的命题是必然的，

因为被罗巴切夫斯基改变之后的

第五公设（平行公里），

本身就与日常生活经验不符。例如，

过平面上直线外的一点，

怎么可能作出多条不同的直线，

与已知直线不相交呢？

由此而建造出来的数学大厦，当然是个怪物。

又如，

罗氏几何导出了如下古怪命题：

一个三角形的三个内角之和，小于180度……

这种奇怪的“几何大厦”，有什么用呢？

有人嗤之以鼻，心想，

不过是疯子数学家玩的游戏而已！

那些嘲笑罗巴切夫斯基的人没有想到，

几十年后，‘非欧几何’在爱因斯坦的

广义相对论中找到用武之地，

‘非欧几何’正是广义相对论描述的

弯曲空间所遵循的几何！

🎂 几何上的无穷小

不过，真正与弯曲空间有关的是

“黎曼几何”，

黎曼几何比上面所说的‘罗氏非欧几何’更进一步，

因为“黎曼几何”属于‘微分几何’*。

【*微分几何是运用微积分研究空间的几何性质的数学。

    古典微分几何，研究三维空间的曲线、曲面；

    现代微分几何研究更一般的空间--

    流形空间（后述）。 

微分几何与拓扑学*等数学分支有紧密联系。

广义相对论就是以微分几何作为数学基础的。

*拓扑是研究几何图形或空间

在连续改变形状之后，还能保持性质不变的

学科。参见下面视频】

欧几里德之后，笛卡尔发明了解析几何*

（在中学课本中，解析几何被解释为：

采用数值的方法来定义几何形状，

并从中提取数值信息。

这种数值的输出可能是一个方程或者是一种几何形状）。

牛顿和莱布尼茨发明了微积分。

两者的结合

使得那个时代的物理如虎添翼，面目一新。

像罗巴切夫斯基那样使用传统的公理方法

研究几何，显然要比较落后了。

克莱洛以及高斯等人，认识到这一点，

创立并发展了微分几何。

微分几何的先行者、法国克莱洛（1713 - 1763）

对空间曲线进行深入研究，

第一次研究了空间曲线的‘曲率’和‘挠率’。

什么是‘曲率’和‘挠率’呢？

我们从图1a所示的三条平面曲线来认识曲率。

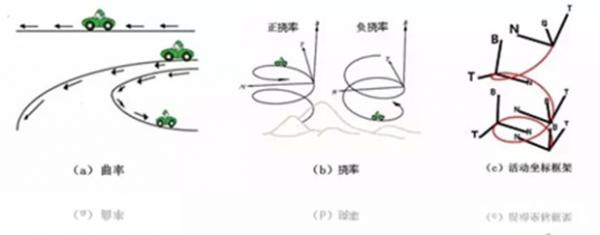
   图1：曲线的曲率和挠率

图中三条曲线，就像是三条形状不同的

平地上的高速公路。

我们还需要引进曲线的切线，或称之为

“切矢量”。切矢量，即是，当曲线上两点

无限接近时，两点连线的极限位置所决定的矢量。

图1a所示的公路上标示的‘箭头’，

便是在曲线上各个点‘切矢量’的直观图像。

曲率是什么呢？

曲率表征曲线的弯曲程度。

比如，图1a中最上面一条公路是直线，

直线不会拐弯，我们说，

它的弯曲程度为0，即曲率等于0。

‘切矢量’转得越快，曲线的弯曲程度也越大。

‘切矢量’，说白了，

就是汽车在公路曲线上弯曲的那一个点。

数学上把曲率定义为‘切矢量’对于弧长的旋转速度。

平地上弯弯曲曲的公路，可以看作是‘平面曲线’，

用“曲率”可以描述它们。

如果公路修在大山之中，

公路会一边转弯、一边还要盘旋向上（或向下）。

这时候，汽车驶过的路径便不再是‘平面曲线’

而是‘空间曲线’了。

对于山间公路，如图1b所示，

我们除了可以看到其弯曲的程度外，

还能观察到公路往上（或往下）绕行的快慢。

我们将这个描述绕行快慢的几何量，叫“挠率”。

（一条‘空间曲线’的曲率和挠率）

空间的变化规律，决定了这条曲线的状况。

从上面对‘空间曲线’的初步介绍，

可以看出，‘微分几何’方法，

比‘欧氏几何’公理方法要细致精准。

与曲线类似，

‘微分几何’可以用在研究曲面上，

曲率和挠率概念，能推广到曲面上，

科学上

曲率和挠率可以定义复杂得多的曲率张量

【在微分几何中，‘曲率张量’，即黎曼张量

是表达流形曲率的方式——详见后面】

   未完待续，谢谢。