“人生就像一场旅行,不必在乎目的地, 重要的是沿途的风景及看风景时的愉快心情。
《广相论之15·内蕴性几何 》 前面我们说到,对‘空间曲线’(二维)的研究, 是用‘微分几何’的方法, ‘微分几何’比‘欧氏几何公理’要精准得多。 同时,‘微分几何’还可以用在 对‘空间曲面’(三维)的研究上。
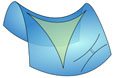
一个三角形,沉浸在一个鞍形面上,图上还有两条发散的超平行线。 马鞍面上的几何,就是前面介绍的罗巴切夫斯基几何,又被称为‘双曲几何’。
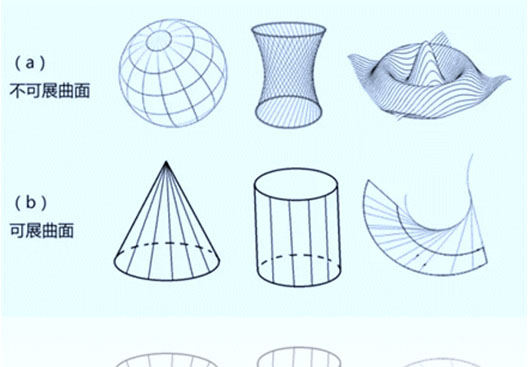
‘空间曲面’的形状,可以分为两大类:
a.不可展曲面; b. 可展曲面。 初看 图2 a 和 图2 b 所画的曲面, 也许看不出这两类图有什么区别—— 认为不管可展还是不可展, 看起来都是“弯曲”“不平的”。 但是,如果仔细观察,就会发现, ‘可展曲面’的“弯曲” 与‘不可展曲面‘的“弯曲”有着本质的区别。 简单地说,
可展曲面在本质上是“平的”,
它们可以被展开成一个平面。
比如,将图2 b所示的锥面
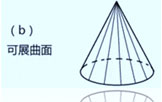

用剪刀剪一条线直到顶点,
就可以没有任何皱褶地将它平摊到桌子上。
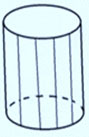
柱面也可以沿着与中心线平行的
任何直线剪开,成为一个平面。 但是,图2a所列举的‘不可展曲面’, 就不能展开成平面了。 那是真正的、本质上的“不平”。 一顶做成了近似半个球面的帽子, 你无论怎样剪裁它, 都无法将其没有皱褶地摊成一个平面。

另一方面,你用一张平平的纸, 很容易卷成一个圆筒(柱面)
或者是做成一顶‘锥形帽子’ 。


但你无法做出一个球面来。 你顶多只能将这张纸剪成许多小纸片, 粘成一个近似的球面! 谈到这儿, 大概已经明白“可展”和“不可展”的区别了。 尽管两类曲面在嵌入3维空间后, 看起来都是弯曲的,但是, ‘可展曲面’的内在本质是“平的”; 不可展曲面的内在本质是“不平”。
区分这两类曲面的“内在本质”, 叫“内蕴性”研究, 研究这种性质的几何,叫‘内蕴几何’。 黎曼几何就是‘内蕴性几何’。 曲面的内蕴性最早被“数学王子”高斯所注意, 后为黎曼所发展,并推广到‘大于3’的n维流形* 【*流形(Manifolds)
是局部具有‘欧几里得性质’的空间】 黎曼几何就是一种‘内蕴几何’。
换言之,内蕴性指的是 曲面(或曲线)不依赖于它在三维空间中嵌入的方式。 也就是说, 内蕴性是曲面某些内在的、本质的几何属性。 高斯用曲率,来表征曲面的这种特性。
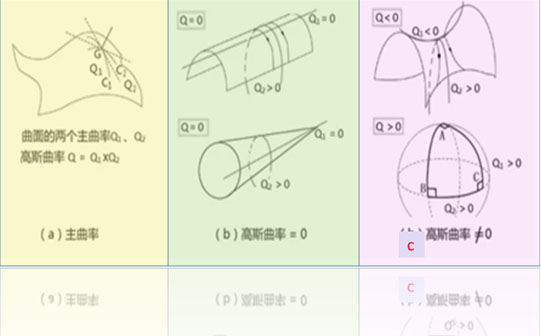
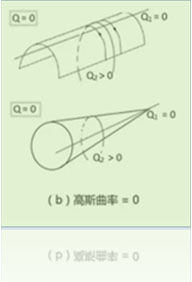
如果一个曲面的曲率为0,
说明它本质上是平的,是可展曲面, 如图3b(淡绿色部分)所示。
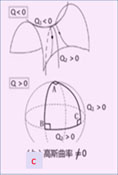
如果一个曲面的曲率不为0,
说明它本质上是不平的,是不可展曲面, 如图3 c(粉色部分)所示。
Q 代表曲率符号。
曲率不为0的情形又有两种。 正的高斯曲率对应于球面几何(图3c的下图); 负的高斯曲率对应于马鞍面(图3c的上图)。 更正:原图(b应该改为c。编者已经改过来了。) 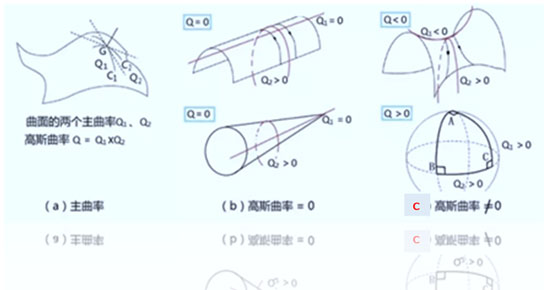
图3:曲面及曲率 未完待续

|
