友好提示: 完整版共分第一部和第二部。 2部相加共43分钟,谢谢。

饱受地震、海啸、洪水、粮食短缺、
人口爆炸、疾病与战乱灾难中的人类, 如何在百苦齐降的大淘汰来临前, 选择一条正确的道路,才能幸免于难?
——《创世纪·诺亚方舟现世?》记者黄凯熙


《玛丽或汤姆如何在弯曲空间平移》
如何判定我们所面对的是哪一种几何呢?
最简单的办法是 测量该曲面上三角形的3个内角之和是多少度:
(1)‘平面几何’的 3个内角之和应该是 180度(平面几何就是欧式几何); (2)‘球面几何’的 3个内角之和应该是 大于 > 180度(球面几何属于黎曼几何); (3)‘双曲几何’ 的 3个内角之和应该是 小于 < 180度(双曲几何即罗氏几何)。

一个观察者在自己生活的空间所能够观察 和测量到的几何性质,就是这个空间的内蕴性质 (广义相对论中,曲率是最常见的内蕴性质)。 比如说,球面的内蕴性质, 就是生活在球面上的2维爬虫感受到的几何性质。 我们人类是3维生物,不是什么2维爬虫。 但是,因为我们的地球很大, 我们的肉身的尺寸比起地球来说太太小了。 因此,我们可以将自己想象为某种 2 维生物 (请暂闭双眼,想象一下把自己的肉身 放在地球上—— 地球的体积,可是有约1万亿千米3)。 在相对论里, 一个观察者, 他在自己所处的空间所能做的几何测量, 只能是内蕴性质的测量 (研究曲面的“内在本质”,叫“内蕴性”研究)。 比如,一个在卷曲白纸上生活的小虫儿, 它通过测量可以得出自己所在的空间是欧式几何, 即曲率为零。 但是如果在三维空间的人看来, 这张白纸却是弯曲的。 我们在地球上测量一个大三角形
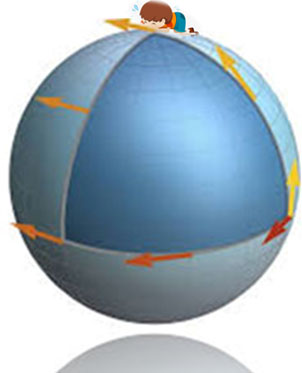
如图中的球面三角形, 测地员将发现,这个三角形的三个内角都是90度, 因此,内角的和 = 270度,即大于欧式几何的180度。
图3 c下所显示的是一个规则球面,
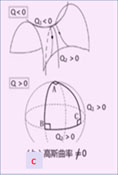
规则球面的空间弯曲程度,到处都一样, 但一般来说,许多空间的弯曲程度 却不一定处处相同, 于是数学家就用“平行移动”概念, 来帮助研究空间的弯曲情况。 那么,究竟什么是广义相对论中的平行移动呢? 简单地说,广义相对论中的平行移动 就是将一个矢量*平行于自身的方向, 沿着空间里一条曲线的移动。 就像汽车上的陀螺仪那样, 汽车沿公路运动时, 陀螺仪总是平行于自己原来的指向。
【*矢量,即向量。 物理学上指由大小和方向共同决定的量。 如力或速度等。】

汽车陀螺仪能提供精确的测量结果, 可提升汽车导航仪和远程信息处理系统的推算。
在物理上,大家感兴趣的是: 一个向量平行移动一圈,回到原点时, 它的方向是否会改变?比如说, 跟着汽车转一圈的陀螺仪,它所指的方向, 是否还和原来出发时的方向一样? 也许你会不加思索说:当然没变。 这是因为你习惯了用‘欧氏空间’的 直角坐标系来考虑问题。 如果我们假设地面是一个欧几里德平面, 陀螺仪平行移动回到原处时,方向的确不会改变。 但是,每个人都知道,地球是一个球体, 所以我们实际上是生活在一个球面上。 那么,如果从球面(或者别的曲面)的角度 来研究这个问题,又会得出什么样的结论呢? 如前述,所谓“平行移动”是说, 在移动向量时,尽可能保持向量方向、 相对于自身,没有变。 弯曲空间的平行移动,好比一个人 平行地前进、后退、左右移动, 只要他的身体没有(额外多地)扭动, 就叫平行移动。 这样,当他移动一圈儿回到出发点时, 他认为他应该和原来出发时,面对着同样方向。 如果他是在平面上移动的话, 他的这个想法是正确的。
但是,如果他是在球面的弯曲空间移动的话, 他希望保持与自己原来的向量方向平行的情况, 但是实际上他是沿着球面空间的曲线,在平行移动, 他将发现自己朝面的方向就不一样了! 出发时,他的脸朝左;回来时,脸朝前,如下图
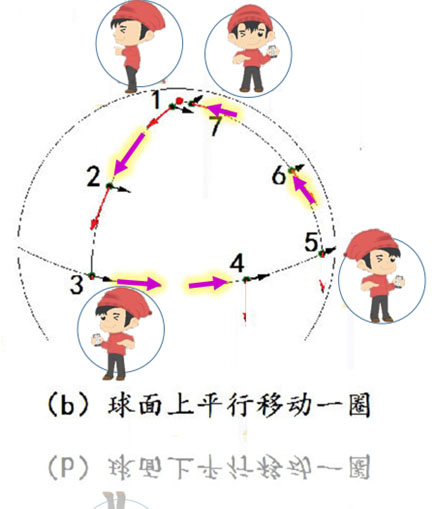
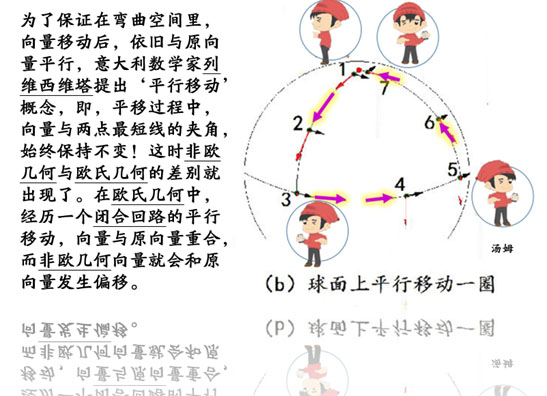
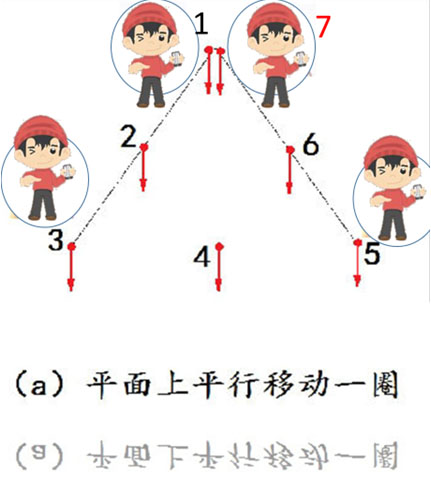
未完待续。谢谢阅读。
|
