5分钟

2分钟
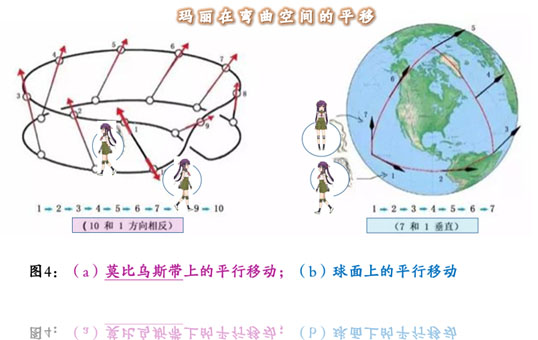
假如将玛丽面对的方向用一个箭头(矢量或曰向量)来表示, 上图左边所示的是一个矢量在莫比乌斯*带*上的平行移动, 当矢量从位置1出发,沿着数字1、2、3……一直移动到10, 也就是回到原来的出发位置时,得到的矢量与原来的反向。 而上图右边所示的是球面上的平行移动, 当矢量从位置1出发,沿着数字1、2、3……一直移动到7, 也就是回到原来的出发位置时, 得到的矢量和原来的矢量形成垂直方向。
*莫比乌斯带,是一种只有一个面(一个表面) 和一条边界的曲面,也是一种拓扑结构*。 它是由德国莫比乌斯和李斯丁在1858年独立发现的。 这个结构可以用一个纸带,旋转半圈, 再把两端粘上后,轻而易举地制作出来。
【说明】
在数学上,球面上一个向量*, 沿着‘闭环路’平行移动。 这个向量所转过的角度α ( 阿尔法) {displaystyle alpha }, 与闭环路内部的面积——成比例。 *向量(也称矢量),指具有大小和方向的量。 它可以形象化地表示为带箭头的线段。 箭头所指:代表向量的方向; 线段长度:代表向量的大小。 与向量对应的量叫做数量(物理学中称标量), 数量(或标量)只有大小,没有方向。《百科资料》 通常人们所理解的平行线不是非欧几何概念的。 欧几里得几何是平面几何, 所说的平行线是相对平面而言的, 而非欧几何中的平行线是相对曲面而言的。 为什么曲面几何中 “过(所谓)直线外一点, 连一条平行线也引不出来”? 这得拿地球仪做参考, 因为球面是弯曲的, 球面上两点之间的最短距离是大圆周—— 用球面上的两点和球心三点做一个平面, 截出的那个圆周就是大圆周 (大圆周也叫短程线)。 黎氏几何中的短程线, 就类似于欧氏几何(平面几何)中的直线。
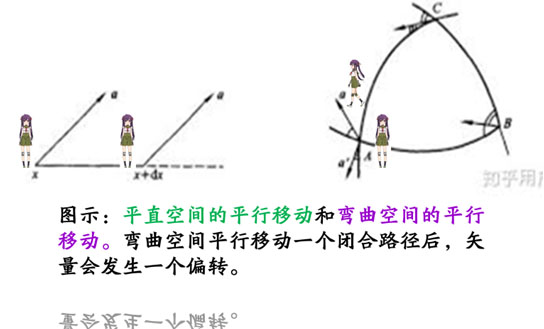
【图示】 平直空间的平行移动和弯曲空间的平行移动
在弯曲空间,平行移动一个闭合路径后,会发生偏转。
上面两个例子说明, 在曲面上平移一圈儿后,不能保持原来的方向, 而是出现与出发时的方向有偏差的情况。 这个偏差与曲面的‘曲率’有关, 反映了曲面的弯曲程度。
3分钟 *拓扑是研究几何图形或空间在连续改变形状后还能保持不变性质的一个学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。
谢谢。
|
