35分

12分

萨哈罗夫在这片所谓“爱国者”的汪洋大海中，

像一叶孤舟，随时都要被愤怒的群众淹没。

但是，知识分子干什么来的呢？

就是要用智慧和良心引导民众呀。

阿扁历险记

     ——再释弯曲空间的平移

如前述，所谓弯曲空间的‘平移’，

就是将一个矢量（向量），

平行于自身的方向，沿着空间一条曲线的移动。

在平坦的欧几里德空间，这种移动是一目了然的。 

现在想象有个极小、极扁的

二维平面生物“阿扁”，

阿扁生活在一张平面纸上。

阿扁很聪明，他会用坐标系。

阿扁感受到的几何，是欧几里德几何，

即他感受到，

三角形的3个内角之和，等于180度，等等。 

阿扁学过微积分、会计算许多图形的面积，

自然也懂得矢量（向量）等概念。

阿扁所理解的平行移动，

就是像下图左边所示的：

矢量（向量）移动时，

要保持与自己原来的方向平行。

如何做到这点？

即，只要保持

这个矢量在直角坐标系的分量不变就可以了。

分量是个常数。

在图中，直角坐标系是以红色大十字表示的。

那么，到底什么是‘分量’呢？

通俗地说，

分量，即向量在X轴或Y轴上的投影。

当选好坐标系后，向量就可以分解、

或者说，向量就可以‘投影’在坐标轴上，

向量在坐标轴上投影的大小，即是向量的分量。

投影 ，指图形的影子投到一个面或一条线上。

从初中数学角度说，

用光线照射物体，在某个平面上

（地面、墙壁等）得到的影子，叫做物体的投影，

照射光线叫投影线，投影所在的平面叫投影面。

呆在平面纸上的阿扁发现，

如果将向量沿着一条‘闭曲线’平行移动一圈，

再回到原来出发点的话，

向量的大小和方向不会改变，

经过平行移动得到的向量和原来的向量一模一样。 

不过有一天，来了一个3维世界的小生物“阿三”，

阿三看见阿扁生活的这张纸，

他突发奇想，把这张纸剪去一个角。

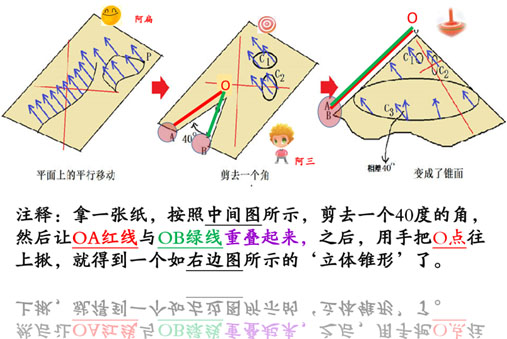
比如说，像下图‘中图’所画的情形，

阿三在纸上剪去一个40度的角，

然后将剩余图形的两条‘红绿剪缝’黏在一起，

做成一个像下图右边所示的锥面。

天道酬勤（这是一定的）：

您可以起身去拿一张纸，按照中间图所示，

剪去一个40度的角，之后，用手把O点往上揪起来，

就得到一个如右边图所示的立体锥形了。

这时生活在纸上的小小阿扁，

没有感到他的世界有什么变化。

在阿扁看来，他周围的世界仍然是平平的，

那条红色直角坐标轴几乎纹丝不动地

呆在原地。当阿扁拿着他的（平面）陀螺仪  

沿着小圆圈C₁或C₂作平行移动

回到原来出发点时，

陀螺仪的指向和原来一样。

这说明向量平行移动的规律没有改变。

不过，阿扁的技术越来越高，

胆子越来越大，旅游的地点也走得越来越远。

他逐渐发现一些问题。比如说，

当他沿着右图中所示的曲线C₃走了一圈，

回到原来出发点时，

他的陀螺仪的指向和出发时候

有了一个40度的角度差

这个40度的差，

是根据锥形几何及微积分公式算出来的。

这个发现让阿扁激动，

于是，他进行了更多的平行移动实验，

绕了好多不同的圈，终于总结出一个规律：

他生活的世界，在右图中所标记的点O附近，

有一个特殊区域，

只要他平行移动的‘闭曲线’包含了这个区域，

陀螺仪的指向，

就总是和原来出发时的方向相差40度。

如果不是绕着这个区域转圈的话，

平行移动便不会使矢量的方向，发生变化。

当时的阿扁，技术还不够精确，

还没有搞清楚这个区域是多大，

况且，他也有点害怕那块神秘兮兮的地方，

不敢在那儿逗留过久，作太多的探索，

以防遭遇生命危险。

阿扁喜欢读书学习新知识，

他从一本数学书中了解到，

如果陀螺仪走一圈方向改变的话，

说明自己所在的空间是弯曲的。

因此，通过对多次实验结果的总结，

阿扁提出一个假设：

他所在的世界基本是平坦的，

除了那块奇怪的区域外！

再回到我们的世界来看球面几何。

陀螺仪走一圈后方向改变的值，

叫做平移一周后产生的‘角度亏损’，

可用θ表示

（国际音标/ˈθeɪtə/ 近似音‘塞它’）

角度亏损与空间曲率有关。

一个标准球面上的曲率处处相等。

如果有某种生活在球面上的扁平生物的话，

他沿任何曲线绕行一圈后，

陀螺仪方向都会有变化，

而且，

‘角度亏损θ’（‘塞它’）是不固定的，

‘角度亏损θ’

与绕行回路所包围的球面面积成正比。

阿扁想通了这些道理，

明白他的世界大多数地方都是平面的，

只有一点不对，

那一点附近的空间是弯曲的锥面。

锥面是一个可展曲面。

它所有地方的几何

都与平面上的欧几里德几何一样，

除了那个顶点以外。

也就是说，锥面上每个点的曲率都等于0，

但顶点是一个曲率等于无穷大的奇点

（奇点是指在时空的曲率无穷大的那一点。

   在奇点所有的定律都失效。）

这时阿扁恍然大悟：

原来我生活在一个锥面世界！

        ——以上源自张天蓉博客。

为适合更多人观看，

引用时有‘些微’增删或改动。

5分钟

 谢谢。