亲爱的朋友，在前一篇博文中，

我们说到，对于曲面上某个切点G，

通过旋转（像旋转木马那样）可以形成无限多面。

过切点G、且与切平面垂直的那条线

叫‘曲面在点G’的法线。过法线可作无限多法平面。

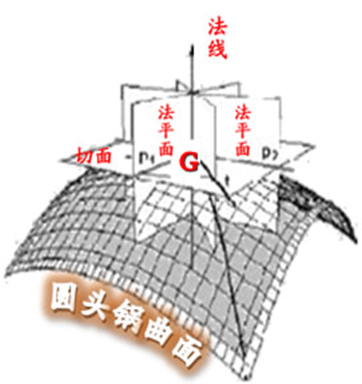
【友好提示】

以上叙述有 2个要点

（1）不要把曲面想象成是二维的；在这个例子中，

曲面是三维空间中那个鼓鼓地倒扣着的圆锅曲面。

【倒扣着的圆锅的曲面】   

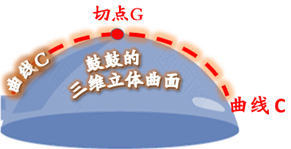
（2）叙述时心中不要忘记

         所有的变化都是过 G 进行的。

补充注释：曲面有二维、也有三维的。画在纸上的曲面是二维曲面，而空间的曲面是三维曲面。例如，雨滴或肥皂泡一类的曲面，就属于三维曲面。

好了，现在您可以再次想象

那个圆锅上的生日蛋糕，

拿一把小刀去切蛋糕—— 

蛋糕的主人，人缘很好，过生日这天，来了许多人，

并且每人都想分一块蛋糕，通过这种分享

与主人一起欢度快乐时光……。

故事中的蛋糕

可以魔幻般地被切成许多块儿，

每个小块都有刨切面 ，

于是大蛋糕就出现了许多刨切面。

‘剖切面’原本是为了绘制剖视图所使用的假象平面。

   剖视图是用于表达物件内部结构的形状的，

   剖视图是假想的平面或曲面。

每一刨切面都与下方那鼓鼓的三维曲面，

有一条过G点的相交切线，

过 G点 能画出无限多曲面曲线，

因而也能画出无限多切线

（所做切线均需过G点）。

如果您还想像不出来。

那就再想一个球，然后鸟瞰这个球，

或者想象自己借助神力，飞到天花板

从高处往下看这球的上半部，

这时，你还可以看到有水从切点G处，

紧贴球面往下流，从而在球面上

会形成许多水流的曲线，

重要的是，每条水流曲线都各有各的切线，

（这些切线的一端都被切点G 拽着），

通过以上想象，如果还不明白，

那就先放下，等到以后有兴趣时再来学习吧。

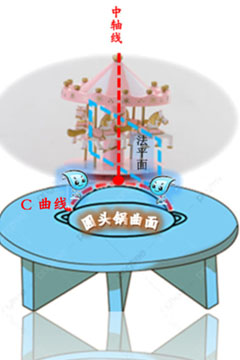
就是说，图上的C曲线，

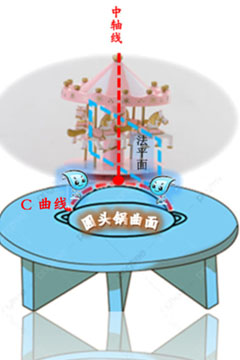
可以把它想象成由蛋糕流出的水滴汇聚而成的水流，

C曲线就像水流，缓缓沿着‘圆锅的三维曲面’，

顺势流下，于是我们可以说

曲线C 的弯曲度是在G点的曲率（如图所示）。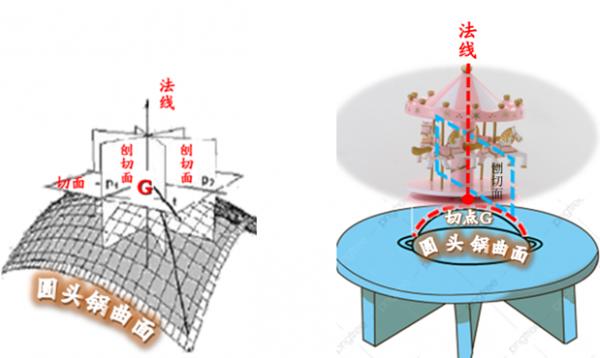

（补充说明：切线 C 可以参看下图）

 谢谢。