25分

 地藏菩萨说 ：

“地狱不空，誓不成佛。

   众生度尽，方证菩提。”

《 场方程和微分几何· 广相论37》

  6、场方程和微分几何

场方程是建立在微分几何（Differential Geometry）基础上的，

微分几何水平不行，

对一些概念是难以理解的。

对微分几何，

爱因斯坦也是在创立场方程过程中，

向他的数学家朋友现学的。

微分几何是运用微积分

来研究空间几何性质的数学。

古典微分几何起源于微积分，

内容是曲线论和曲面论。

欧拉、蒙日和高斯，是古典微分几何的奠基人；

而近代微分几何的创始人是黎曼。

黎曼在1854年创立了黎曼几何，

黎曼几何是近代微分几何的主要内容。 

欧拉（Euler，1707－1783），瑞士数学家。

蒙日（Monge，1746～1818），法国数学家、化学家和物理学家。

高斯（英语：Gauss 1777－1855）， 德国数学家、物理学家、天文学家。

黎曼 ( 1826—1866 )，德国数学家

通过学习，我们了解到，

场方程的计算，离不开黎曼几何

（黎曼几何就是弯曲空间几何）。

1916年爱因斯坦创立了‘引力场方程’，

引力场方程是一个二阶张量方程，

或者说，引力场方程是一个

二阶非线性偏微分方程*。

场方程是用‘张量微积分’表述的。

所谓‘张量微积分’

就是用张量场表述的微分方程。

 【回顾与复习】

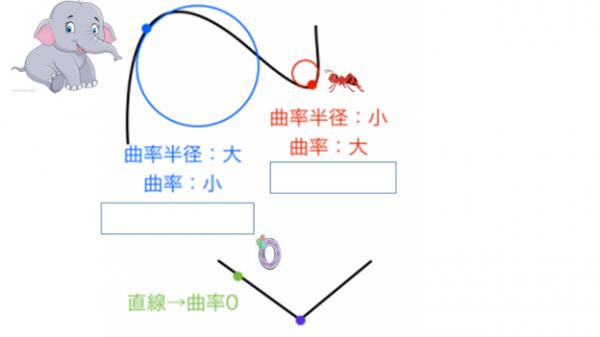
假设弯曲空间，有两个点靠的很近，

就可以把它写成微分形式

（例如，可以把微小距离写成ds 形式。

就是说，数学符号ds表示空间弯曲程度的极小距离）。

在微分几何中，

求弯曲空间曲线的长度（弧长），

需要先定义

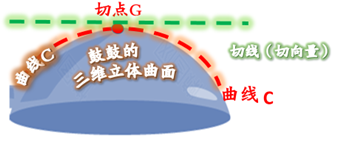
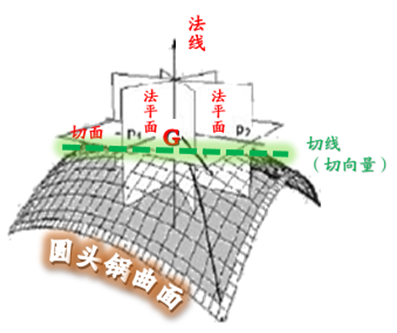
某一点的‘切向量’长度（参看下面3幅图），

然后把这条‘切向量’所经过的

所有‘微元距离’ds，用微积分算一下，

就可以求出特定的线段或角度来。

就是说， 场方程

包含了运用曲线坐标的微分计算

从而得出弯曲时空的曲率。

曲线在某点的切向量可以理解为

沿曲线在该点的切线方向的向量。

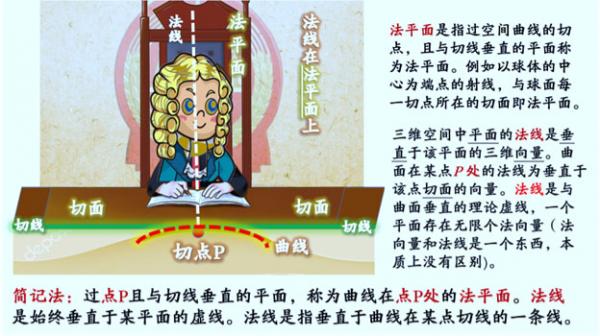
切向量是与曲线相切的向量。

可以通俗理解为

切向量是与法线相互垂直的线，

即曲线的法线是垂直于切线的。

    谢谢阅读。