一,庞加莱不懂语法 1,庞加莱猜想的内容为: 任何一个单连通的,闭的三维流形一定同胚于一个三维的球面。 2,主项与谓项 主项中有【三维流形】,还有修饰限定主项的定语:单连通和闭流形。 谓项中有【三维球面】。 3,庞加莱猜想的主项与谓项的关系 在数学中,三维球面是一个具有三个维度的几何客体,这样的几何客体都可以归类为三维流形。 就是说,主项的内涵与外延全覆盖谓项。 4,当主项与谓项具有同样的概念内涵和外延,我们不是采用证明,而是采用种加属差定义的方法。 所以,将庞加莱猜想(命题)用定义方法:三维球面就是一个单连通的闭流形的三维流形。 5,庞加莱猜想的主项与谓项是:a,种属关系;b,是一种真包含关系;c,是传递关系。 全称判断的命题通常涉及到一个总体的所有成员都具备某项性质,如果主项包含谓项,就会以偏概全。例如“所有的学生(外延宽的)都是小学生(外延窄的)”。这种命题要求对一个整体的每一个成员进行描述,而种属关系描述的是部分与整体的关系,无法准确反映全称判断的逻辑要求,是以偏概全。因此,在逻辑推理中,种属关系不适用于全称判断的命题。 6,数学中的种属关系用定义解决。类似的定义:素数就是大于1并且只能被1和自身整除的自然数(定义是已经搞清楚的内容,将自然数划分为:自然数1,素数,合数)。 我们不能用命题形式:任何大于1并且只能被1和自身整除的自然数都是素数(命题是有待于证明的问题)。 判断,必须有两个以上的不同概念;全称判断的主项与谓项必须是两个内涵完全不同的概念。而庞加莱猜想的主项与谓项是同一概念的内涵。 7,主项的功能和谓项的概念 主项表示判断句子主要说明的人或事物;谓项说明主项的动作,状态或特征-行为-属性等。 真包含关系用于判断,常常出现错误:例如“所有的学生(外延宽的)都是小学生(外延窄的)”。 庞加莱猜想就是这种错误。把本应“所有的s是p”,说成”所有的s是s的一部分“ 8,判断句子主项不能包含谓项。或者说命题的主项不能包含谓项。 数学命题的谓项一般说主项有多少或者主项是什么性质,,例如命题【素数有无穷多】(主项“素数”与谓项“无穷多”是全异关系,素数是名词,无穷多是量词;又例如命题【e是超越数-或者说e具有超越性】,(主项”e“与谓项“超越性”在证明之前是全异关系,因为,e指自然对数的底数,是名词,e是一种实数;超越指一种属性,也是名词。在证明之后是交叉关系)。 9,庞加莱猜想的主项与谓项不是全异关系,而是真包含关系。庞加莱猜想是一个病句。 看到没有?一个错误的句子不具备判断的功能。
数学证明不能用一个猜想去证明另外一个猜想,这是一种预期理由的逻辑错误。 一般认为,庞加莱猜想作出巨大贡献的,主要是瑟斯顿(Thurston),他给出了几何化猜想,认为三维空间一定由八种基本拓扑形状构成。 演绎推理,就是从大范畴中找到小范畴的推理。只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。 演绎推理,就是从大范畴中找到小范畴的推理。只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。 任何一个单连通的,闭的三维流形一定同胚于一个三维的球面。 三维球面(英文常写作3-sphere)是球面在高维空间中的类比客体。它由四维欧几里得空间中与一固定中心点等距离的所有点所组成。寻常的球面(或者说二维球面)是一个二维表面,而三维球面是一个具有三个维度的几何客体,这样的几何客体都可以归类为三维流形。 主项:单连通的,闭的三维流形;谓项:三维的球面。 主项几乎等于谓项,同语反复,没有意义。如果非要证明,只需通过种加属差方法定义即可。 数学界认为,8种构造中有7种不是单连通的,所以剩下的球形就是单连通的。
大前提:瑟斯顿三维空间有8种拓扑形式(A)。
小前提:其中7种不是单连通的(O)。
结论:所以只有球形是单连通的(i)。
这种AOI推理形式是错误的,因为三段论规则之一,前提中有否定判断,结论只能是否定判断,不能得出一个肯定判断。
或者使用相容选言推理否定肯定式: 大前提:8种结构或者是单连通或者不是单连通。 小前提:有7种不是单连通的。 结论:只有球形是单连通的。 推理好像没有问题,但是,这里有3个概念:三维流形;单连通;闭。 第一,在三维流形下列出8种结构; 第二,是否也应该将所有的单连通结构列出来,如果只剩下三维球形才能算数。 第三,还有闭和有界条件下列出其它特征。 数学界认为,8种构造中有7种不是单连通的,所以剩下的球形就是单连通的。 大前提:瑟斯顿三维空间有8种拓扑形式(A)。 小前提:其中7种不是单连通的(O)。 结论:所以只有球形是单连通的(i)。 这种AOI推理形式是错误的,因为三段论规则之一,前提中有否定判断,结论只能是否定判断,不能得出一个肯定判断。 另外,在之前,1961年斯梅尔宣称证明了五维和五维以上成立的结论。1981年弗里德曼宣称证明了四维成立的结论。 问题1,:什么是4维和5维? 几何学家从来没有正确定义过。只有3维和3维以下有明确的文字定义和几何画面定义。 有谁能够画出一个4维或者5维空间结构,并且说明是在3维结构基础上的合理解释。 下面是瑟斯顿给的8种宇宙构造: 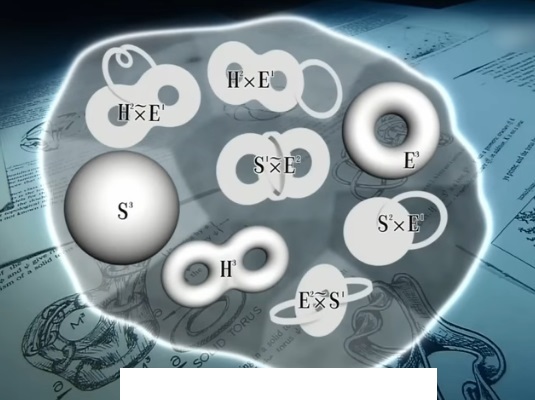
详见本人拙作【空间的维度】 https://blog.csdn.net/2401_85303946/article/details/140303392
数学界用一个猜想(瑟斯顿8种构造的推论)去 证明 猜想(庞加莱猜想)当然是荒唐的(预期理由的逻辑错误)。这个又叫套叠猜想,即猜想中的猜想。大猜想还没有证明,先去证明大猜想中的小猜想(老和尚给小和尚讲故事,从前有座山,山里有座庙,庙里有个和尚在给小和尚讲故事,...。)。佩雷尔曼(Perelman)宣称完成了瑟斯顿“几何化猜想”的证明是不完全的,只能说完成大猜想内的小猜想,只有大猜想成立小猜想才有可能成立;说是这8种构造中有7种不是单连通的,只有剩下的球形才是单连通的。首先排除了其它7种结构,再肯定剩下的球形。
2002 年 11 月 12 日,佩雷尔曼在 arXiv.org 上公布了自己的证明,并在之后半年中又发布了两篇系列论文。这三篇文章概述了庞加莱猜想以及更一般的几何化猜想的证明,从而实现了哈密顿(Hamilton)提出的纲领。并利用几何化猜想证明了庞加莱猜想。 以上的工作纯属胡说八道。 -我们知道,数学家群体普遍的精神疾患和智力低下,根本不具备多次连续正确推理的能力。 |
