日前所发文章“也谈乘法表述及交换律”在朋友中散发传阅后，得到了积极的反响和支持，也有不同的意见反馈。笔者又做了进一步的了解与思考，制作了乘除法算理的示意图，加写了“情境教学可否取代算理”的一段。由于内容的扩充，思考的深入，标题也改了。本文包含前一篇的全部内容，阅读本篇即可。

也谈乘除法算理及其功用

沈乾若

乘法表述是否应该区分被乘数与乘数，是小学数学争论的一个焦点。2001年颁布的《全日制义务教育数学课程标准》，将传统的“被乘数×乘数=积” 的表述改为“乘数×乘数=积”。著名留美数学教育专家马立平博士形容此举“打掉了支撑着大半壁算理体系的承重墙”。而倡导方则辩称这座承重墙并无必要，新的乘法表述更符合乘法交换律。

本文对被乘数与乘数的区分和乘除法算理系统作进一步的探讨，希望算理更为简洁，协调一致。并对当下依赖情境教学、取消算理体系的作法提出了质疑。当然，本文的出发点是基础数学教学，而非数学理论。

一．被乘数与乘数的区分

数学知识源于生产和生活的实际，也在物理等学科之中孕育发展。

在小学引入乘法运算，是从“一行栽树8棵，3行可以栽多少棵？”、“一盒鸡蛋12个，5盒几个？”这类计算物体个数的实例着手的。这里，被乘数与乘数的区分清清楚楚。

到小学高年级和中学，乘法的涵义很快深化，应用范围将大大拓宽。尤其物理学科中，例子比比皆是：

例1. 密度与质量：铁的密度为7.87克/厘米³，计算一个1250厘米³铁块的质量。

算式：7.87g/cm³ ×1250cm³ = 9838g

例2. 匀速运动：一辆汽车每小时行驶75公里，7小时行驶多少公里？

算式：75km/h × 7h = 525km

例3. 热容量与温度变化：一壶水的热容量为5230焦耳/摄氏度，将水从20⁰C烧开，需要提供多少热量？

算式：5230J/⁰C × (100-20)⁰C = 4.184 x 10⁵J

三例中，被乘数分别为密度，速度和热容量；乘数为体积、时间和温度变化；而作为乘积的质量、路程和热量，则是乘法运算的目标和结果。参与运算的，是一个个完整的物理量；不但数字，单位也在其中。乘数的单位通过约分都被约掉，留下的恰好是乘积的单位。单位体现的是一个物理量的量纲，告诉人们它是什麽；甚至比数字更为重要。

从以上三例可见，被乘数与乘数量纲不同，意义不同；更不要提牛顿第二定律F = ma、欧姆定律 V = IR等公式中的质量与加速度，电流与电阻等各种不同的物理量了！

比照以上三例，“一行栽树8棵，3行栽多少棵？”的算式为“8棵/行×3行=24棵”；“一盒鸡蛋12个，5盒几个？”应写作：”12个/盒×5盒=60个“。即使最简单的例子，乘法中的被乘数与乘数各自也具有不同的单位，承载不同的意义。二者的区分乃客观存在，并非人们所强加。

再者，3个鸡蛋加2个鸡蛋等于5个鸡蛋；然而3个鸡蛋不能乘2个鸡蛋。每碗3个鸡蛋乘两只碗是可以的；正如速度可以乘时间，密度可以乘体积，热容量可以乘温度变化；等等。相加的通常是同一集合的元素，而相乘的一般属于不同的集合。故加法不必区分被加数与加数，而被乘数和乘数的区分则有它的道理。

事实上人们争论比较多的，是相乘的元素在乘法算式中的顺序。国内规矩，被乘数在前而乘数在后，写错扣分没商量；尽管交换位置并不影响结果的正确性。这种做法让人感觉过于刻板，带来取消被乘数与乘数区分的变革。

英语中，被乘数为Multiplicand, 乘数为Multiplier；区分是显然的。但算式怎样写则未完全统一；有的先写被乘数，有的先写乘数，不像国内那般严格。写前写后毕竟是人订的规则，有商讨的余地。同时也有的教科书采用“因子x因子=积”的表述，对二者不加区分。

二． 乘法表述的承重墙和三层台阶

小学数学中，从计算物体个数的简单实例入手引入乘法，得到的传统表述为：“每份数×份数=总数”，它相当于“被乘数×乘数=积”，但意义更为清晰。这一表述提供了对乘法的实质性理解和把握；而且简单明了，小学生容易懂，也利于牢固掌握。

然而，这一表述是否可以涵盖意义较为复杂的乘法？譬如，前面的三例乘法是否符合这一表述呢？

首先考查三例中的被乘数：密度为单位体积的质量，速度为单位时间驶过的路程，热容量为物体温度每提高一度所吸收的热量；将它们抽象为“每份数”是恰当的。而作为乘数的1250厘米³、7个小时和80个摄氏度的温度变化，可以说都是“份数”。故三个乘法算式均契合“每份数×份数=总数”。与刚引入乘法时不同的只是，每份数、份数和总数不限于整数。

其他如“加速度×时间=速度变化”，“压强×面积=压力”,“功率×时间=功（或能量转换）”；等等，均为“每份数×份数=总数”的模式。至于牛顿第二定律, 欧姆定律等公式，尽管表面上不易看出；细究起来，亦暗含该模式，或其延申和变形。这一点此处不赘。

可见，小学数学中，从计算物体个数抽象得来的“每份数×份数=总数”的表述，不但揭示了乘法的实际意义，而且为日后理解科学中更复杂的乘法预留了空间。

数学与科学中新概念的建立，众所周知，依据的除生产与生活实践外，还有已确立的概念。乘法即建立在加法的基础之上。引进乘法之初，很自然地将其解释为“若干相同加数之和”。其中加数为被乘数，加数的个数为乘数；如前所述，清清楚楚。此为理解乘法的第一个台阶。

但这样的解释，第一只适用于乘数为整数的情况，第二未能深入乘法的本质。切实理解乘法，须上升到第二层台阶，即“每份数×份数=总数”。这一表述提供了对乘法的实质性理解和把握，提升了思维；是比“相同加数之和”更为到位的解释。

用此表述，作为乘法的逆运算，除法的算理水到渠成：总数除以份数为等分除，总数除以每份数则为包含除。

将乘法延伸到分数与小数，用此表述亦轻而易举。譬如6 x 2/3，按照“被乘数×乘数”的顺序，解释成每份6个，2/3份。而2/3×6 的意思是每份为2/3, 共6份；意思也很清楚。若再以6个2/3相加来解释，好比上了第二层台阶又退下去，从第一阶卖力跨到第三阶，没有道理。

可见，小学乘除法的教学中，“每份数×份数=总数”的表述发挥着重要作用，“承重墙”的说法不为过。

那麽，什麽是乘法概念的第三层台阶呢？乘法的核心，无非一个“倍数”概念，包括分数、小数或百分数作为倍数。乘法即“求某一数量的若干倍”。这个第三层台阶，是我们的目标，也是每个懂得基础数学的人所理解的乘法。

上到了这一层，含分数和小数乘除法的解释简便易行，甚至不必拘泥于“每份数x份数=总数”。分数作除数的算理是一个难点，但用倍数概念解释起来却颇为简单。以4 ÷ 2/3为例，可以有两种解释。对应于包含除的是，求4为2/3的多少倍？另一种，一个数的2/3是4，求这个数，则对应于等分除。

抽象化、一般化是数学的目标。由“相同加数之和”， 到“每份数×份数=总数”，达到“求某一数量的若干倍”；乘法表述的这三层台阶，由简单到复杂，由具体到抽象，由个别到一般；为学生思维的训练和素养的提升提供了一段科学的路径。

三. 乘除法算理的图示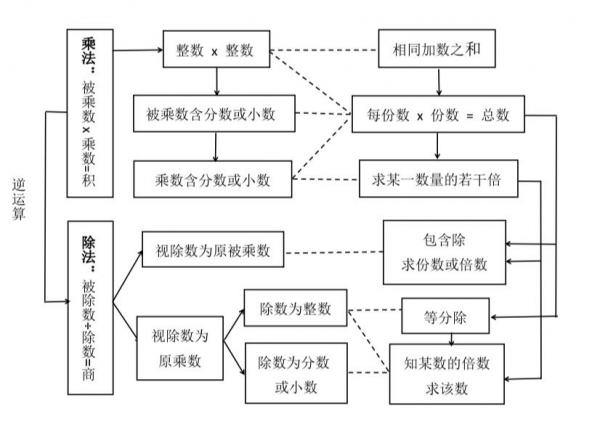

综合以上论述，乘除法的算理可用上面的示意图来表示。示意图左半部分为乘除法的各种运算；右半部分为算理，即运算的意义。虚线表示二者的对应关系。箭头表示运算及其算理是怎样层层递进的；就乘法而言，即前面所说的三层台阶。

示意图清楚地揭示出从整数到分数和小数各类乘除法运算的涵义，及各部分之间的逻辑关系；它们构成一个有机的整体。

两点说明。第一，笔者并非认为此图所示为唯一正确的乘除法算理。若能进一步简化、优化，使之更为和谐一致，当然最好。第二，乘除法算理遵循人们的认识过程，主要是为初学者预备的。算理的讲解须融入运算的学习，为理解运算服务。万不可将算理当作另一套理论灌输给学生，要求学生死记硬背，从而加重他们的负担。

四． 关于乘法交换律

取消被乘数与乘数的区分，倡导者的依据是乘法交换律。我们来看一看这样做是否合理。

先定义乘法，才谈得上两个数能否交换。“一行栽树8棵，3行栽多少棵”与“一行栽树3棵，8行栽多少棵”尽管结果相同，毕竟先要懂得并算出24棵，才得到答数相同的结论。定义乘法而以交换律为依据？逻辑上不大说得通。

3个8和8个3皆为24，确实很简单。然而，在初学乘法的小孩子脑中，这样说不无几分抽象，需要以实物来支撑。故我们只能从“一行栽树8棵，3行栽多少棵”这样的情境着手。

交换律适用于纯数字相乘。或者说，交换律只是在做数值计算时可以使用。在实际问题中，交换被乘数与乘数的数字结果相同；但这样做除极少数情况外，要麽改变了情境，要麽失去了意义。

面积计算似乎是支持交换率的一个较强的例证，属于前面提到的“极少数情况”。如一张长30cm、宽20cm的纸，面积的计算：30cm×20cm = 600cm²，或 20cm×30cm = 600cm² 均可。但若这样端给小学生，他们不一头雾水才怪！学生能够接受的讲法是：：1cm²是边长为1cm的小方块；把纸分为30行，每行宽1cm；得知每行有20个方块，乘以30行，从而算出600cm²的面积。故算式为：30cm²/行×20行 = 600cm²。请看，被乘数与乘数的区分绕得开麽？

再者，本文讨论的乘法为标量相乘的基本运算。以后的数学或物理课还会学习矢量乘法，甚至矩阵相乘，等等。其中有的交换律成立，如矢量之间的点乘；有的不成立，如叉乘。故即使不考虑单位，交换律于乘法也并非理所当然，需要十分注意。

五．情境教学可否取代算理？

课程标准规定不再区分被乘数和乘数之后，小学数学教材中只剩下“乘数×乘数=积”的表述，及倍数和平均分等若干概念的说明。传统的算理体系消失殆尽，新的体系却无踪影；连“除法为乘法的逆运算”都未提及。

这很自然。“乘数×乘数=积”的表述并未提供有实际意义的信息；很难用来解释分数或小数乘法；更不用提解释除法，特别是作为难点的分数除法了。

那麽，我们的教学是如何让学生懂得乘除法，并且能够加以运用的？

翻开时下的小学数学课本，笔者不禁暗暗吃惊。目之所及，处处是图画，描绘日常生活、动植物、科技知识等各种各样的场景。实例之丰富、具体、直观，洋溢着以前的教材所没有的气象，更远非国外的教科书可比。

本世纪以来的新课改强调“创设情境”，这一说法来自美国，来自西方。然而事实上，国外数学教材纯数学的成分居多，应用题在数量和种类方面都差得远；即使小学数学也存在这一问题。“情境创设”仍然不足，“问题解决”更未落实。由于缺少实例的支撑，应用题从来都是难点。不会应用除法，在国外中小学生中非常普遍。

国内则真刀真枪，实实在在下了功夫。教材中成千上万的实例，其背后的工作量非同小可。国内教育界付出的巨大努力，由此可见一斑。

回到我们的问题：国内学生是怎样学会乘除法的？

没有了算理系统，教科书和教师授课通常依据具体情境给出解释，并确定运算方法。比如从运动类题目得到“速度×时间=路程”的公式；求速度时则用路程除以时间。从购物类题目得到“单价×数量=总价”，那麽总价除以单价则得到数量。又如，由除以2相当于乘以1/2, 推出除数为分数的情况下颠倒相乘的计算方法。至于一个数除以分数的实际意义，则避免做一般性的讨论。

正是在众多实际情境的浸润之下，学生得以懂得乘除法，基本上掌握了它们的应用。

然而，抽象化、一般化、培养逻辑思维能力乃数学的宗旨；情境教学而不提升到一般性规律，我们是否走向了另一个极端？是否有偏离数学正轨之嫌？尽管每一部分的解释都有道理；但支离零散，缺少关联，不成系统的解释，终归差强人意；达不到数学的目标与应有的境界。

人认识事物的过程包含一往一返的两个阶段，第一阶段从个别到一般，从具体到抽象，得出概念与理论；第二阶段从一般到个别，从抽象到具体，验证和应用理论于实际问题。第一阶段的思维方式是归纳、猜想之类；第二阶段则主要为演绎思维。演绎推理乃数学中大量训练的思维模式。

显然，没有提升到一般性规律的情境教学，不完整、不到位，也缺少演绎推理的训练。具体到乘除法，缺了算理，学生可以应付一般的题目，但欠缺解决深层次问题的能力。

数学归根结底玩的是概念。“需要逐步养成从概念出发思考和解决问题的习惯，概念缺失对后续数学大厦的建立是有较大影响的”，数学教师杨磊如是说。

2023年6月

鸣谢：

本文在写作过程中笔者与杨磊、韦炜进行了讨论，吸收了他们的观念；特此致谢。

同时感谢张景中院士的指导和启发。

    作者简介：

    沈乾若，北京大学物理系毕业，北京航空航天大学工学硕士，加拿大西蒙菲沙大学数学博士。《加拿大博雅教育学会》名誉会长，《融汇中西教育论坛》召集人。具备中国大陆和加拿大数十年大、中学教学及办学经验。现为独立教育学者，从事比较教育研究。研究方向为教育体制与政策，基础数学与科学教育。