《迈克摔下后说,脚疼……》
(12) 演算在继续…
现在让我们提前看一下 历史上已经被推导出的贝尔不等式: 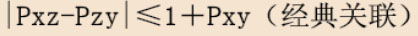
如今 我们已经有了 Pxz 等式、 Pzy 等式 和 Pxy等式,有了这 3 个宝贝 再考虑到所谓‘贝尔不等式’的关联 (关联,指 ☞ 爱因斯坦所主张的世俗世界的关联):
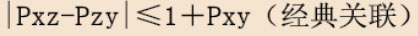
就需要先将 Pxz 等式减去Pzy等式,同时还要 取其‘绝对值’(| |)
得到:
|Pxz-Pzy| =|-2N3+2N4+2N5-2N6| =2 |N3+N4-N5-N6|
(这个结果也是按照前面介绍的 那种概率上的加减规则 以及同类项合并等原则得出的)
由于这个式子很重要, 我们就给它起个有绰号吧, 叫什么好呢? 就叫‘男女不论高矮’吧
(X可以代表人的性别, Y代表高矮,Z代表眼睛的颜色, 由于 Pxz 和 Pzy,都有一个 Z, 前后相减,可以略去),
好,现在这个‘不论高矮’式, 已经被我们推出来了, 但是这个式子 实际上是一个有关‘绝对值’的式子, 那么,什么是‘绝对值’呢? 所谓‘绝对值’是指不计正负的实数值。 例如,实数 A 的绝对值,记作|A|。 ‘正数’或‘零’的绝对值就是它本身; ‘负数’的绝对值是它的相反数。
关于‘绝对值’, 我们有绝对值关系式,如下:
|x-y|≤|x|+|y|
我们可以把这个式子想象成: 如果从一大堆糖果(x)里, 刨去一小堆糖果(y),其结果会怎样呢? 其结果就是这些‘劫后余生’的糖果, 必然是‘小于’一大堆糖果 (x) 再加一小堆糖果 (y) 的 ; 那么如果从一大堆糖果中 刨去 0 堆糖果, 则一大堆糖果 必然是‘等于’ 一大堆糖果 + 0, 这可是很容易懂的哦。 好了,言归正传, 我们若把‘绝对值关系式’ 套用到前面的那个 叫‘不论高矮’式子里, 就可以得出 一个‘不论高矮’的扩充式:
|Pxz-Pzy|=2|-N3+N4+N5-N6| ≤2(|N3+N4|+|N5+N6|)
这个结果 也是按照‘概率上的加减规则’ ‘同类项合并规则’ 以及有关‘绝对值公式’推出来的。
其间特点: 道理浅显,过程繁复。
接下来,让我们回忆一下
概率中有关“1”的等式是:
1= N1+ N2+……+N8,
于是我们可以从前面那个繁复的式子里, 经过观察,凑出一个等于‘1’的式子来, 然后再将这个等于‘1’的式子, 带进相关式子里, 从而得出一式,这个式子就叫
2 乘以‘吧啦吧啦 ’= 1 加上‘呼噜呼噜’式:
2(N3+N4+N5+N6) =1+(-N1-N2+N3+N4+N5+N6-N7-N8)
这个式子的推演特点仍是,道理简单,过程繁复。 回过头来, 再来看前面有关 Pxy 的式子, 在前面曾经说过, 《概率表》中的(Pxy) 即‘人的高矮概率式’, 于是,可以写成:
Pxy=-N1-N2+N3+N4+N5+N6-N7- N8
那么, 前面那个 2 乘以‘吧啦吧啦’ = 1 加上‘呼噜呼噜’中的‘呼噜呼噜’式, 正好是等于 Pxy ! 所以我们最终得到:
|Pxz-Pzy|≤1+Pxy
这就是量子力学史上的
“贝尔不等式”了。 若将“贝尔不等式”画成彩图形式
即是
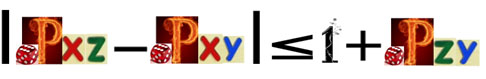
把这个形象化的不等式, 写成数学形式是: 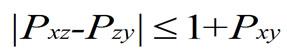
那么 这个式子到底是什么意思呢? 在流行理论中,
X 、Y、Z并不代表
2类量子宇宙人的性别、高矮或眼睛的颜色,
在学术文章中,
X、Y、Z的意思
分别表示A或B粒子
在三维坐标系所测量到的自旋状态, 例如Pxy的意义是表示“ A在x方向上”
和“ B在y方向上”这2者之间的相关系数。
在统计学中,
‘相关系数’用于度量
两个变量X和Y之间的相关性,
即相关系数是衡量
两个随机变量之间的
相关程度的。 比如我们生活在3维空间,
就可以在3个方向上进行观测,
我们把这3个方向假设为x,y和z。 Pxy代表A粒子在x方向上
与
B粒子在y方向上的相关性。 在爱因斯坦的隐变量中,
认为两个粒子无论是否观察它们,
它们的状态,
从分裂的一瞬就已经是确定的了。 隐变量认为,
假如物质世界没有超越光速的信号传递,
那么,当我们同时观察两个粒子的时候,
它们之间是无法交换信息的,
它们所能达到的协作程
度,仅限于经典世界所给出的关联 这个关联就是
用经典方法推导出来的贝尔不等式。
【感想,百人中或许不会有太多的人, 会舍出时间一步步推演 (即使名著也会在繁复的推演中有笔误, 例如《上帝掷骰子吗》PDF版 第193页正数第5行就有笔误, 即:式子中N3前应是减号;N5前应是加号)】
好了, 现在我们至少可以从公式的推演中, 先了解一下大概的意思, 并且明白若按照“贝尔不等式” 做量子实验(来验证)的话, 那么量子实验的结果表明, 贝尔不等式不成立。
就是说,
在经典物理中,贝尔不等式成立,
但在量子世界中,贝尔不等式不成立。 亲爱的朋友, 笔者本来记忆力还不错, 但是经过这一番推演, 已累得两眼冒金花了, 昏沉中,想长久地记住 这个本来就很拗口的定理很难。 于是想了一个窍门, 把‘贝尔定理’戏称为:
世俗社会,不公平成立; 量子世界,不公平不成立。 OK!
如此,
在昏昏欲睡中也能记住它哦。

哎,人在懵懂中来、又在懵懂中去, 虽快活一时, 却终不知自己究竟活在怎样一种世界……, 物理学家告诉我们, 没有人能懂量子力学所描述的世界, 但我仍要说, 即使是盲人摸象 做一个真诚的探索者也是值得的,不是吗? 推荐:
《上帝掷骰子吗—量子物理史话》曹天元著
PDF版第190-193页 以上图片参考网站约为: wtoutiao.com//www.nature.com//www.cartoonlogodesigns.com //www.suggestkeyword.com//www.123rf.com//www.jpppt.com//www.taopic.com //www.wikihow.com//www.qqbaobao.com//ask.goodbaby.com//www.1zc.net //www.diyifanwen.com//p.twipple.jp//www.hihol.com //www.nipic.com //www.mises.org.br //1643177797.jpg//i.mtime.com ////weili.ooopic.com //www.tooopen.com //www.tooopen.com //www.wikihow.com//www.dianliwenmi.com //wuxin20070717.blog.163.com//sucai.sioe.cn //i.mtime.com www.tupian114.com //sucai.redocn.com//www.nipic.com //www.ooopic.com 0dao9deshuzikatongtupian.sokutu.com////www.utu123.com cn.depositphotos.com //www.nipic.com //wuxin20070717.blog.163.com 谨此致以谢忱!
|
