 今天我在公司上网搜索时,发现谷歌的搜索网页改变了logo的图像,谷歌经常采用这种方来纪念一些历史上的重要人物。今天(2011年8月17日)是纪念法国的大数学家费尔马(Fierre de Fermat)。点击这个图像之后,谷歌搜索列出这位数学家的有关网络结果。 今天我在公司上网搜索时,发现谷歌的搜索网页改变了logo的图像,谷歌经常采用这种方来纪念一些历史上的重要人物。今天(2011年8月17日)是纪念法国的大数学家费尔马(Fierre de Fermat)。点击这个图像之后,谷歌搜索列出这位数学家的有关网络结果。
我对于这位大数学家倒是一点也不熟悉,但是有关数字的各种游戏和命题在我小的时候曾是我所憧憬的科学研究,虽然当时正值文化大革命时期,学生罢课闹革命,整个中小学曾处于瘫痪的状态。但是当时我对所有十分稀少的课外读物,尤其是数学的东西都十分钟爱,记得当时曾把过去的《十万个为什么?》系列书也列为禁书,但我家还是保留了数册,这些书曾是我的珍宝,读了不知多少遍,我和许多很好的朋友经常交流,经常激动地分享和争论。后来邓小平恢复高考之后,我们这些上山下乡的知青对知识出现从未有过的饥渴,到处寻找各种科学和数学的补充资料,如饥似渴地大量贪梦汲取,在短短的时间里拼命补充各种渠道所能得到的知识,各种数学的趣题和难题都对我产生过大的吸引力。也正是这种动力和拼命地学习,我非常荣幸地以高分考被为数不多北京最高等学府所录取,从此改变了我的一生。
一晃眼几十年过去,历史是这么的具有讽刺性,看看现在的中小学生有这么好的环境和条件,可他们却对学习是那么地麻木,当然这有非常复杂社会原因,其中有来自社会和家长的巨大压力,这种极大反差的极大转变,造成现代学生们再也没有我们过去那种的饥饿感、缺乏对学习那种发自内心的热情和旺盛的精力。
回到数学话题,我对数字和各种有趣的难题和命题都仍然保持有十分的兴趣,最近我写了一篇有关视图乘法算数的故事,并由此我产生联想到编程中经常遇到的数字溢出问题,接着我花了两三天的业余功夫,由视觉乘法的启发用JavaScript写了一个小程序,结果我可以计算任何两位正整数的乘法,永远不会有溢出,当然这只是一个编程的游戏。正是我对数学和编程独有钟情,因此特别喜欢利用编程编写程序来解决各种过去我曾无法解决的有趣问题。现在,我一直寻求一个算法求解所有答案的难题所困扰(目前还需保密),不过逐渐有了一些眉目,我将用iPhone平台将我的算法设计为一个有利于大脑锻炼的计算游戏。
我经常与我朋友和同事交谈这些有趣的话题,演示我的成果,他们都十分欣赏我的才能(也许这里我有点自卖自夸了)。不过我的确一直还是对一些数学的难题保持童年的那种热情,我经常告诉我的同事,应该将这些有趣的内容通过讲解和挑战的方式传播给我们的下一代,让他们也有我们童年、甚至像费尔马那些人一样,对科学和数学永远保持那种坚持不懈的探索态度,这对于他们的将来发展将会是十分有益的。
谷歌的这种对名人纪念的方式,以历史来回顾和教育我们如何欣赏前人的丰功伟绩,同时激励我们和下一代利用更为优秀的条件,开创出更为美好的未来。
最后,提及一下费尔马,他实际上本不是一位职业的数学家,但他对数学有特别的兴趣,他致力于数学的探索和研究,提出了许多世界级的数学命题和解答,他的有关质数理论是目前电脑中加密的最好随机序列(怪不得谷歌今天纪念他),他还是微积分和统计学的开创始祖之一,他的许多成果都是他钟爱数学的结果。
谷歌采用的图像是他著名的命题:如果n>2,找不到有任何三个整数能使下面的命题公式成立(^为幂次方):
x^n + y^n = z^n
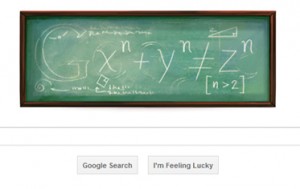 这一命题357年后由英国的数学家Andrew Wiles证明。
我的RSS |
