中国科学院智慧火花：http://idea.cas.cn/viewdoc.action?docid=67996

黎曼猜想：

黎曼ζ函数，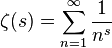  

非平凡零点(在此情况下是指s不为-2、-4、-6···等点的值,S=X+Yi, X=1/2)的实数部分是½

一，黎曼猜想逻辑结构的主项是一个集合概念
【（主项】：所有的非平凡零点（函数） 

【谓项】：位于直线，1/2+yi的临界线上。

主项“所有的非平凡零点”是一个集合概念：

（一）概念的划分：
    （1），单独概念和普遍概念
a，单独概念，反映独一无二的概念，单独概念的外延只有一个。例如，上海，孙中山，，，。它们反映的概念都是独一无二的。数学中的单独概念有“e”“Π”。“e是超越数”就是一个单独概念的命题。
b，普遍概念，普遍概念反映的是一个对象以上的概念，反映的是一个“类”，这个词项的内涵由为了包含在词项外延所必须具有的事物的性质组成。例如：工人，无论“石油工人”，“钢铁工人”，还是“中国工人”，“德国工人”，它们必然地具有“工人”的基本属性。数学中的普遍概念有例如“素数”，“合数”，等。“素数无穷多”就是一个普遍概念的命题。
数学证明对象全部都是普遍概念或者单独概念。
（2），集合概念和非集合概念。
a，集合概念反映的是集合体，这个词项的外延由词项所应用的事物集合组成，例如“中国工人阶级”，集合体的每一个个体不是必然具备集合体的基本属性，例如某一个“中国工人”，不是必然具有“中国工人阶级”的基本属性。集合概念的命题是不需要证明的，也是无法证明的，只能是归纳总结。
b，非集合概念（省略）。

（二），不同概念的公式

1，普遍概念命题公式

     公式中没有变量，或者有变量n并且可以无穷大，但是根据计算结果可以判断事物的性质，是普遍概念命题公式。
普遍概念的公式，在计算之前，就知道了计算结果的性质。

2,集合概念命题公式

“某个事物（某个形式）的所有元素或者多个元素具有某种性质” 的判断。这个例如，欧拉在1772年素数公式，是一个集合概念公式：

 的值都是素数。对于前几个自然数n = 0, 1, 2, 3...，多项式的值是41, 43, 47, 53, 61, 71...。当n等于40时，多项式的值是1681=41×41，是一个合数。实际上，当n能被41整除的时候，P(n)也能被41整除，因而是合数.。

   集合概念的公式不能保证计算结果具有这个公式想要的结果性质，是一种不确定的结果公式。因为集合概念的每一个个体不是必然具有这个概念的基本属性。这个公式是一种形式上的集合，就是全部具备这种形式。



      因为，主项是集合概念的命题是无法证明的，因为集合概念的每一个个体不是必然具有这个概念的基本属性。就决定了必须一个个去证明。

 二，黎曼猜想是一个二阶逻辑问题

 黎曼猜想的所有 “零点” 也是一个集合，零点是这个对象上的函数，按照通常数学中定义，一个n元函数就是从论域A的个体的所有n元组的集合至A的一个映射。当我们用“所有个体”、“存在个体”，量词加在论域的个体上，称为一阶量词。“

   “ 所有函数”、“存在函数”、“所有关系”、“存在关系”是二阶量词，即二阶逻辑。黎曼所说的“所有零点”就是“所有函数”的二阶量词，黎曼猜想已经超出了G弗雷格建立的一阶逻辑形式系统（即谓词演算），涉及极为复杂的逻辑系统，一般的数学家对此毫无所知。

    举一个例子：“加速度”不是一个基本量，即不是长度或者质量什麽的，而是一个变化率，还是二阶变化率，即变化率的变化率。

       黎曼猜想就是：所有的A（零点）成立的充分必要条件是包含在A中的B（x+yi，x=1/2）成立。即变化率B的变化率A成立，所以只能一个个地验证，无法一次性证明。

三，以往的证明都是错误的

    在证明黎曼猜想的历史中，美国莱文生1974年宣称证明“至少”有34%的零点成立是荒唐的，因为这是一个特称判断，说明莱文生证明必然错误，并且在集合概念前面加数量词34%，也是一种语法错误。

  一个笑话：“小张经过一年努力掌握了1000多个英语词汇”。词汇是集合概念，表示一种语言词项的总汇，前面不能用“1000多个”限制。中国也有两个数学家楼世拓姚琦，1980年宣称证明了“至少”有35%的零点成立，纯属无稽之谈。以及更加荒唐的张益唐说自己有信心证明，真是没有最sb，只有更sb。

作者在德国，黎曼的家乡