哥德巴赫猜想是说:每一个大于2的偶数都可以表示成为两个素数之和 第一部分、素数的公式 公元前300年古希腊的埃拉托斯特尼创造了一种筛法,可以产生任意大的数以内的全部素数: 要得到不大于某个自然数n的所有素数,只要在2—n中将不大于 素数的倍数全部划去即可。 素数的倍数全部划去即可。 上述筛法可以总结为 1,如果n是合数,则它有一个因子d满足1<d≦ 。 。 2,若自然数n是一个素数,当且仅当它不能被不大于 任何素数整除,则n是一个素数。)。 任何素数整除,则n是一个素数。)。 可以把2的汉字内容等价转换成为英语字母: 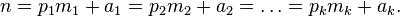 .........(1) .........(1)
其中  表示顺序素数2,3,5,....。 表示顺序素数2,3,5,....。 ≠0。 ≠0。 这样解得的n,若 ,则n是一个素数。 ,则n是一个素数。 我们可以把(1)式内容等价转换同余式组表示: 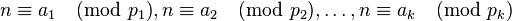 ..........(2) ..........(2)
由于(2)的模 , , ,..., ,..., 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的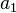 , , ,..., ,..., ,(2)式在 ,(2)式在  ... ... 范围内有唯一解。 范围内有唯一解。 公式计算的范例 例如: k=1时, ,解得n=3,5,7。求得了(3, ,解得n=3,5,7。求得了(3, )区间的全部素数。 )区间的全部素数。 k=2时,  ,解得n=7,13,19; ,解得n=7,13,19;
 ,解得n=5,11,17,23。求得了(5, ,解得n=5,11,17,23。求得了(5, )区间的全部素数。 )区间的全部素数。
k=3时 | 
| 
| 
| 
|  | 31 | 7,37 | 13,43 | 19 |  | 11,41 | 17,47 | 23 | 29 |
求得了(7, )区间的全部素数。 仿此下去可以一个不漏地求的任何给定数以内的全部素数。由孙子定理知,对于所有可能的 )区间的全部素数。 仿此下去可以一个不漏地求的任何给定数以内的全部素数。由孙子定理知,对于所有可能的 值,(1)和(2)式在 值,(1)和(2)式在  ... ... 范围内,有 范围内,有 ( )( )( )( )( )...( )...( )....(3)个解。 )....(3)个解。
以上内容请参见清华大学出版社【品数学】第5页。

第二部分,哥德巴赫猜想的合理框架 (一)怎样使得两个自然数相加和相减都成为素数,即N+X成为素数,N-X也是素数。
根据除法算式定理:“给定正整数a和b,b≠0,存在唯一整数q和r(0≦r<b),使a=bq+r”。
再根据同余定理:“每一整数恰与0,1,2,3,...,m-1中一数同余(mod m)”。所以,任给一个自然数N (N > 4 ),都可以唯一表示成为:

作者在埃及开罗 |
