第一部分 什麽是孪生素数猜想? 素数 与素数 与素数 有无穷多。 有无穷多。
第二部分:孪生素数的公式 利用素数的判定法则,可以得到以下的结论:「若自然数 与 与 都不能被任何不大于 都不能被任何不大于 的素数 整除,则 的素数 整除,则 与 与 都是素数」。 都是素数」。 这是因为一个自然数 是素数当且仅当它不能被任何小于等于 是素数当且仅当它不能被任何小于等于 的素数整除。用数学的语言 的素数整除。用数学的语言 表示以上的结论,就是:
存在一组自然数 ,使得 ,使得

其中  表示从小到大排列时的前k个素数:2,3,5,....。并且满足 表示从小到大排列时的前k个素数:2,3,5,....。并且满足

这样解得的自然数 如果满足 如果满足 , ,则 , ,则 与 与 是一对孪生素数。 是一对孪生素数。 我们可以把(1)式的内容等价转换成为同余方程组表示:  , ,  ,.... , ,.... , ....(2) ....(2)
由于(2)的模 , , ,..., ,..., 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定 都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定 , , (2)式有唯一一个小于 的正整数解。 的正整数解。 第三部分,范例 例如k=1时,  ,解得 ,解得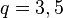 。 。
由于 ,所以可知 ,所以可知 与 与 ; ; 与 与 都是孪生素数。这样就求得了区间 都是孪生素数。这样就求得了区间 里的全部孪生素数对。 里的全部孪生素数对。
又比如k=2时,
列出方程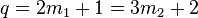 ,解得 ,解得 。 。 由于 ,所以 ,所以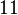 与 与 ; ; 与 与 都是孪生素数。 都是孪生素数。 由于这已经是所有可能的 ,值,所以这样就求得了区间 ,值,所以这样就求得了区间 的全部孪生素数对。 的全部孪生素数对。 由于这已经是所有可能的 值,所以这样就求得了区间 值,所以这样就求得了区间 的全部孪生素数对。 的全部孪生素数对。 仿此下去可以一个不漏地求得任意大的数以内的全部孪生素数对。 对于所有可能的 值,根据孙子定理得知,(1)和(2)式在 值,根据孙子定理得知,(1)和(2)式在  ... ... 范围内,有 范围内,有 ( )( )( )( )( )...( )...( )...(3)个解。 )...(3)个解。 注意,由于 ≠0; ≠0;  ≠ ≠ 是一回事所以第一项( 是一回事所以第一项( )。 )。
第四部分,结论推广
孪生素数猜想就是在k值任意大时(1)和(2)式都有小於 的解。问题已经转入初等数论范围。 的解。问题已经转入初等数论范围。 [中等数学]2000年1期,王晓明


作者在纽约哥伦比亚大学
|
