网传数学家张益唐，已经攻克了朗道-西格尔零点猜想（Landau-Siegel Zeros Conjecture）。

这纯属造孽！

先谈谈证明黎曼猜想的方法问题：

1，证实。这是不可能的！有两种情况：


（1），直接证实！因为黎曼猜想主项是一个集合概念，是一个二阶逻辑问题，是变化率的变化率。是无法一次性证明的问题。只能一个个地验证。

详见智慧火花数学栏目“迈克尔阿迪亚证明黎曼猜想错误百出”；物理学栏目“黎曼猜想与物理学”。
（2），间接证实！证明所有的函数不等于0的情况下（比等于0的情况还要多无穷多个），实部大于（不等于）二分之一。

这个要求与（1）是反对关系，而不能是交叉关系。这里也有无穷多个可能，只能逐一验证，因为主项是一个集合概念，是二阶逻辑问题。

2，证伪。找到一个反例。但是，至今没有找到。

张益唐企图通过证伪的方法，张益唐表示，“如果一个朗道-西格尔零点成立的话，最后能够得出一个不等式来。而这个不等式明显是错的，于是从这里就能够推出矛盾。

从这个角度来讲，我们就从朗道-西格尔零点的存在性，得到了一个矛盾。目前来讲，我能报告的是，至少一个弱形式像这个问题方面，还是有可能做出来，但是整个technical（技术上）的东西是非常复杂的。”【未来论坛|张益唐：数论中的朗道-西格尔点问题】.。

朗道-西格尔零点被定义为广义黎曼猜想的反例，断言此类零点不存在的猜想，就是“朗道-西格尔猜想”。

张益唐想这样证明：

大前提：有一个否定黎曼猜想的Landau-Siegel“点”（特称判断I）。

小前提：这个点不存在（否定判断O）

结论：黎曼猜想成立（全称判断A）。

根据三段论规则，大前提是特称判断，小前提是否定判断，推不出结论。

张益唐采用了错误的三段论格式IOA。


三段论有256个格式，有效格式只有19个。

演绎推理要求两个前提必须是真实的，结论才有效，而张益唐用小前提否定大前提是一个不真实的。

与安德鲁怀尔斯证明费马大定理一样的错误；与迈克尔阿迪亚证明黎曼猜想一样的错误。

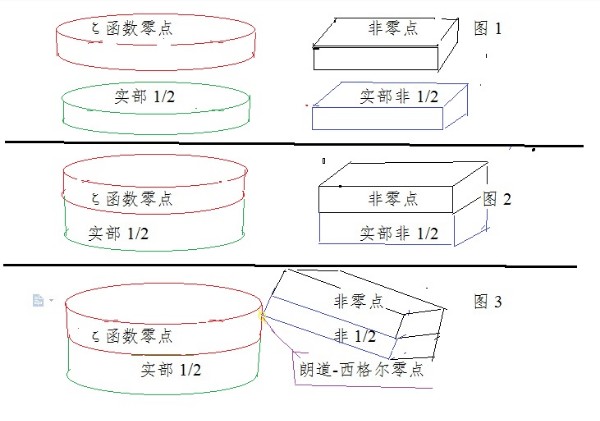
图1（上图）是指：左上是函数零点，左下是实部1/2；右上是非零点，右下是实部非1/2。
图2（中图）是指：黎曼猜想，零点与实部1/2重叠，零点与实部1/2一 一对应；非零点与实部非1/2重叠，即非零点与非1/2一 一对应。
左图与右图是反对关系。

图3（下图）是指：朗道-西格尔零点的实部非1/2。否定了图2黎曼猜想零点与实部1/2会一 一对应。左图与右图交叉关系，哪怕是只有一个“点”。
如果张益唐证明了这个点存在，就是说找到了这个点，也就是反例，即否定了黎曼猜想。
如果没有找到这个点，而是否定这个点，就没有任何意义，因为就是IOA格式。



张益唐论文有111页，这是不可能正确的！

       因为数学目前没有制定推理和证明的规则，对一个问题的论证，三言两语还勉强应付，几十页几百页的推理和证明，没有人不出现错误。

     因为数学没有物质世界检验，不像其他学科可以通过实验来验证，例如物理学的理论对不对，我们通过实验结果就知道了。所以只能通过批判完成证明。自己认识总是片面的，必须由其他人批判才能看到不足和错误。

---------------------------------------------
最后谈谈------什么样的证伪是有效的。

1，最有效的是找到反例。例如，高斯发现费马数在n=0,1,2,3,4时都是素数，如是猜想，n在任何时候都是素数，欧拉给出了n=5时，费马数是复合数。它有一个因数是641.。
2，如果不能找到具体的反例，至少应该构造出一个反例，即自相矛盾的结构，例如欧几里得证明素数无穷多个的反例：N=2x3x5x.....xPn+1。其中Pn表示假定存在的最后一个素数。于是得出矛盾。

只有这两种证伪的方法，不存在第三种方法。安德鲁怀尔斯和迈克尔阿迪亚的证明是无效的，因为他们使用错误格式IOA。

【张益唐造假事件】

https://blog.creaders.net/user_blog_diary.php?did=MzM1NTA5

---------------------------------------------------

张益唐的最新论文表明：

在特定范围内，朗道-西格尔零点不存在。在这一情况下，朗道-西格尔零点猜想正确或成立。

”特定范围內”是一个特称判断，即有些A是B，这是一个数学事实，没有任何意义，因为，数学不承认特定判断的“数学事实”。数学事实是数学理论中最低形式，表现形式是“有些A是B”。数学定理必须是一个全称判断，即一切A是B。
.

为什么数学命题需要证明：

数学第一层次是数学事实，例如3和5都是素数；数学事实都是以特称判断形式出现。表现形式是“有些A是B”

数学第二层次是数学概念，概念是将事实归纳成为一个系统性的含义。是人类在认识过程中，从感性认识上升到理性认识，把所感知的事物的共同本质特点抽象出来，加以概括，是自我认知意识的一种表达，形成概念式思维惯性。例如“孪生素数”；指两个相差2的素数。将数学概念组合成为一个陈述，叫做数学命题。例如“孪生素数有无穷多对”。

数学第三个层次是数学定理，从数学概念和命题到数学定理需要证明。例如欧几里得素数有无穷多个就是一条定理。例如命题“孪生素数有无穷多”，就是还没有得到证明的。

数学第四个层次是数学理论。例如【初等数论】，包括了一系列概念、定理、公式、图像、函数。

第一个层次不会自动上升到第三个层次，必须借助第二个层次即概念，通过演绎法证明完成。

张益唐思维混乱，什么也不懂。完全是胡闹。