四色定理的证明需要语言学家
一,下面是四色定理证明发生的过程:
第1条:平面或者球面苹能画出4个两两相连区域,说明3种颜色对地图染色是不够的(必要条件)。图1 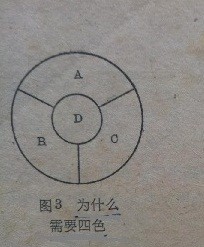
第2条:A德摩根证明了平面或者球面不能画出5个和5个以上的两两相连的区域(充分条件)。 下面是德摩根的证明.图2图3


第3条:
那么地图苹要4种颜色染色(结论)。
第4条:反驳第3条,下面这个图不是4个区域两两相连,依然需要4种颜色(6个区域,需要4种不同的颜色ABCD)。图4,
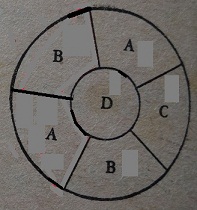
的确,上面这个图不是4个区域两两相连,但是3种颜色是不够的。
第4条不是反例,因为,反例必须是否定一个全称判断的结论。第4条也没有否定前提,苹是增加了前提条件。 问题出在哪里? 图2的所谓“反例”穸x词是: 虽然没有腹造4个区域两两相连,依然需要4种颜色。 那厶,会不会“虽然 法腹造5个区域两两相连,未必就不需要5种颜色”。 前者是“没有腹造”,但是“可以腹造”; 后者是“ 法腹造”。看明白了吗? 如果语言学家再明确一点说明,问题就解角F。 问题在于——需要4种颜色染色的情G有两种: 1,可以腹造4个区域两两相连的。 2,没有4个区域两两相连的。 后者不是前者同一级别,就是说,后者不能代替和否定前者。这个问题搞清楚了,也就是是A德摩根已经证明了四色定理。 同样我们依法炮制图4原理,下面的图,是一个汽车轮胎一样的环面,左面图1有5个区域两两相连,需要5种颜色;右面的图2不是5个区域两两相连,依然需要5种颜色两两相连。 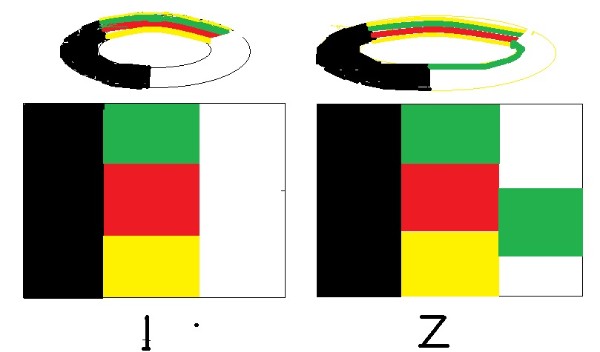
, 未来的工作苹需要搞清楚前提
|
