【数学】最漂亮的数学公式
1988年,德国著名的科学出版社Springer旗下的数学杂志《Mathematical Intelligencer》让读者评选“最漂亮的数学公式【the Most Beautiful Mathematical Formula Ever】”。
读者选出瑞士数学家欧拉(1707-1783)的著名公式“欧拉恒等式(Euler's identity)”为第一名。
欧拉恒等式 - 公式【1】:
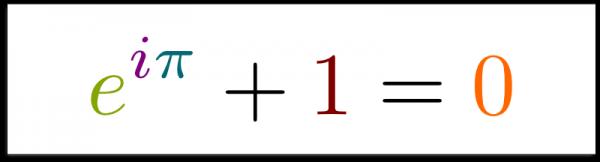
顺便说一下,以上这些读者选出的前5个数学公式里,属于欧拉名下的就有3个。
学过高中数学中的复数知识的都知道,可以用指数函数来表示复数 x+iy(i称“虚数单位”,定义为-1的平方根)。
公式【2】:

这用一个直角坐标图可以看得比较清楚: 【图3】【复数-直角坐标】
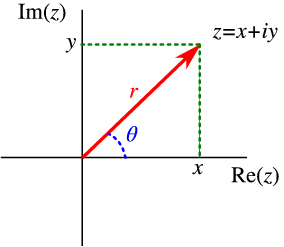
这里, r = √(x^2 + y^2),称“模(modulus)”,φ是点(x,y)和直角坐标系原点的连线,与x轴之间的夹角。
实际上,公式【2】是由以下被称为“欧拉公式(Euler's formula)”的公式【4】推广而来的:
欧拉公式 - 公式【4】
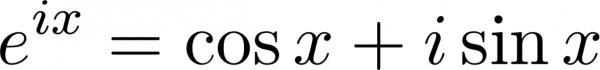
欧拉公式可由级数展开或在公式两边分别求导来证明。
当φ = π 时,欧拉公式(公式【4】)即成为欧拉恒等式(公式【1】)。
仔细琢磨一下,可以看出,欧拉恒等式--公式【1】的漂亮之处在于: 1)实现了指数函数和三角函数之间的量的对应;
2)实现了直角坐标系和极坐标系之间的量的对应; 3)实现了实数和复数之间的量的对应; 4)沟通了似乎互不相关的一些数学常数之间的关系:e、π、i、1和0。
无怪著名法国数学家拉普拉斯(Pierre-Simon Laplace,1749-1827)说过:“读读欧拉,读读欧拉,他是所有人的老师。”
欧拉的所有著作至今尚未整理完毕。估计他的著作全部出齐,可达84卷之多。它们涉及了数学的绝大多数领域,以及物理学和天文学等领域。欧拉的许多工作都是开创性的。
== 相关链接: Euler's identity: https://en.wikipedia.org/wiki/Euler%27s_identity
Euler's formula: http://mathworld.wolfram.com/EulerFormula.html https://en.wikipedia.org/wiki/Euler%27s_formula
Leonhard Euler: https://en.wikipedia.org/wiki/Leonhard_Euler
|
