趣味的数学-466
如图,证明:
【图】 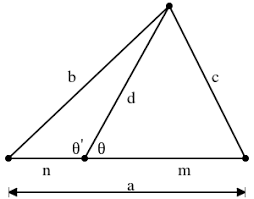
ΔABC的三边边长分别是a、b和c,d是从三角形顶点A出发到长度为a的BC边的一条直线(例如中线和角平分线),且d把BC分为长度分别是m和n两部分,其中m靠近长度为c的AB边,n靠近长度为b的AC边。有: m*(b^2) + n*(c^2) = a(d^2 + mn) 从三角形另外两个顶点B和C出发并分别相交于它们的对边的直线,也有类似的性质。 请利用这个定理,找出三角形中线和角平分线的长度,与三角形三边长度之间的关系。
(高的长度,则可从求三角形面积的海伦公式【Heron's formular】中直接导出。)
|
