【数学】几个2阶等差数列-gugeren-万维博客-万维读者网（电脑版）

网络日志正文

		【数学】几个2阶等差数列	2017-05-27 11:44:57

【数学】几个2阶等差数列

人们对等差数列（又名“算术数列”）非常熟悉。

1,2,3,...,n,...，是公差为1的等差数列，n>=1。

2,4,6,...,2n,...，是公差为2的等差数列，n>=1。

1,4,7,...,n+3,...，是公差为3的等差数列，n>=1。

这里的3个带有n的表达式，称为等差数列的（普）通项。

现在看看另一种数列。

以下4个数列的各项数字，分别整齐地排列起来，可以各自构成一个多面体，故它们也统称为“多面体数（polygonal number）”。

1] 三角形数（triangular number）：其通项T(n)= 1/2 n^2 + 1/2 n（其前5项为1, 3, 6, 10, 15）。

【有关“三角形数”的详情，请看本博博文《有趣的三角形数》。】

2] 平方数/正方形数（square number）：其通项S(n)= n^2（其前5项为1, 4, 9, 16, 25）。

【图1：平方数】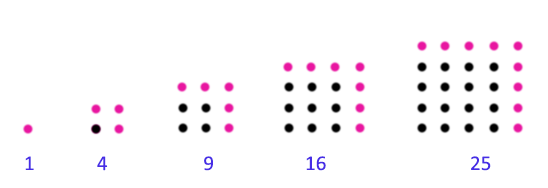

3] 五边形数（pentagonal number）：其通项P(n)= (3/2)*n^2 - 1/2*n（其前5项为1, 5, 12, 22, 35）。

【图2：五边形数】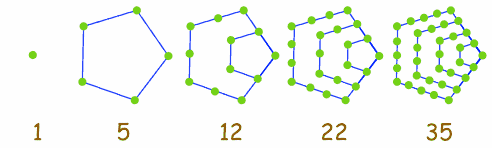

4] 六边形数（hexagonal number）：其通项H(n)= 2*n^2 - n（其前5项为1, 6, 15, 28, 45）。

【图3：六边形数】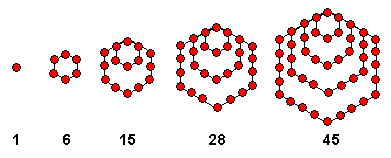

这些数列相邻两项之间的差，称为“级差”。

根据上述4个数列，可以看出，它们的4个级差分别是：

1] 三角形数（triangular number）：当n>=2时，其第n项与第(n-1)项间的级差为 n，它们分别是2, 3, 4, 5, ...。

2] 平方数/正方形数（square number）：当n>=2时，其第n项与第(n-1)项间的级差为 2n-1，它们分别是3, 5, 7, 9, ...。

3] 五边形数（pentagonal number）：当n>=2时，其第n项与第(n-1)项间的级差为3n-2，它们分别是4, 7, 10, 13, ...。

4] 六边形数（hexagonal number）：当n>=2时，其第n项与第(n-1)项间的级差为4n-3，它们分别是5, 9, 13, 17, ...。

容易看出，这些数列两项之间的级差的级差分别是相同的：

数列1] 的两项之间的级差的级差是1。

数列2] 的两项之间的级差的级差是2。

数列3] 的两项之间的级差的级差是3。

数列4] 的两项之间的级差的级差是4。

这就是“2阶等差数列”的定义：由一个数列的级差形成的新的等差数列。这些新数列的通项公式就是原数列的级差。

因此，可以把一般意义上的等差数列看作为为1阶的等差数列。

也可以由此定义更高阶的等差数列，如3阶等差数列、4阶等差数列，……。它们通称“高阶等差数列”。

纵观中国数学史，中国的两宋的数学家沈括（1031-1095）和杨辉（约1238-约1298年），元代数学家朱世杰（1249-1314），以及清代数学家李善兰（1810-1882）等几代数学家，都对高阶等差数列做出了贡献。

欲求各个数列的前k项之和，可先从求数列2]的连续自然数的平方和的前k项入手。这4种数列通项的最高次都仅是2次方，故计算起来不难。

1] 三角形数（triangular number）：其前k项之和S(3,k) = n(n+1)(n+2)/6

2] 平方数/正方形数（square number）：其前k项之和S(4,k) = n(n+1)(2n+1)/6

3] 五边形数（pentagonal number）：其前k项之和S(5,k) = n^2*(n+1)/2

4] 六边形数（hexagonal number）：其前k项之和S(6,k) = n(n+1)(4n-1)/6