一,数学家不是逻辑学家-你们不能跨行业工作-你们无法完成数学命题的证明-你们搞数学证明就是民科 证明一个复杂的命题是一项逻辑学家的工作,你们不是逻辑学家,你们来干数学命题证明,好比钢琴家开飞机,钢琴的键盘与飞机的仪表有本质差别,安全性根本没有保障。 逻辑学上的绝对性证明,难度极大,需要非常高的智商,需要漫长时间的逻辑训练,需要对具体事物的熟悉和严格把控,需要跨越逻辑障碍。 二,什么是数学命题证明的逻辑障碍 数学思维必须符合逻辑,演绎证明某事肯定是这样,归纳说明某事在实际上是有效的,溯因仅仅表明某事可能是,所以溯因是推理中较弱的一种形式。 溯因整理成为一个命题叫做猜想(证明一个猜想是告诉你结果,让你按照规则找出原因-过程的必然性,把道理讲清楚)。我们证明一个数学命题就是一种整体上弱势溯因推理,每一个局部需要强势演绎推理,这是无法克服的困难----超出了人类解决问题的能力!况且,,一个事实可能有多种原因,我们要找到那个必然的原因,并且用演绎推理证明就是它。好比逆水行舟,盲人摸象。 演绎是从一般到特殊,归纳是从很多特殊到某一个一般。但是,溯因逻辑是从一个现象或者一个事实,反推出可能存在的原因。 数学定理必须是全称判断,结论是全称肯定判断的正确三段论只能是第一格的AAA式。这是绝大多数数学命题证明无法做到的。
下图,大前提在哪里?
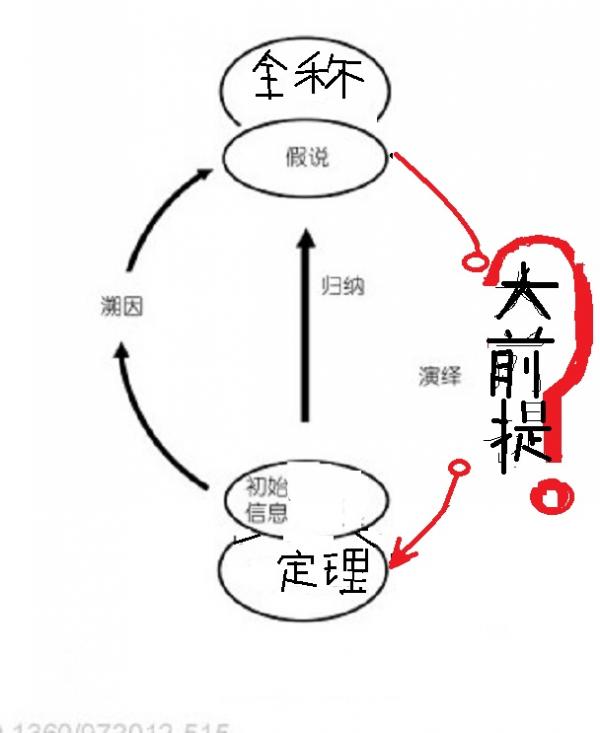
初始信息经过归纳+溯因形成一个全称判断的假说,最后再通过演绎推理证明成为一个定理。将初始信息变成定理,经过演绎推理最困难的就是找到大前提。 这是非常困难的。如果数学命题不是要求全称判断,那么,演绎推理就很容易了,问题在于,数学要求你总结的假说必须是全称判断,你就无法找到大前提。如果天然存在一个大前提,那么问题就很简单。 溯因推理是从结果追溯原因的推理. 溯因推理是关于采纳假说的推理. 采纳一 个留待观察的假说不能被适当地称为归纳, ―但它仍 然是推理, 虽然它的安全性低,虽然从逻辑规则说有一点小小的障碍, 然而它是逻 辑推导, 它仅以疑问的或猜测的方式断定其结论, 它 是真的, 因为它有一种完全明确的逻辑形式.归纳推理是基于有限观察的、从有限样本推出一 般结论的推理, 它的前提是关于个别事物具有某种 性质的论断, 结论却试图得出全体事物皆具有此性 质的论断.。 注意,不完全归纳出来的全称判断形成的待证命题,怎么可能通过演绎推理回到初始信息?让初始信息变成一个定理? 归纳是在一个有穷大的样本中, 只要样本空间没有被穷尽, 使用的都是简单枚举归纳推理. 对于无穷大的样本, 我们根本不可能穷尽该样本空间, 因此只能使用简单枚举归纳推理. 简单枚举归纳推理是一种扩大前提的推理, 它的结论是不可靠的. 使用归纳推理提出假说, 其假说是非常脆弱的, 因为对它的证实是不可能的, 除非你穷尽样本空间, 而一旦如此, 你使用的已经不是归纳推理了. 它的脆弱性还表现在, 只要一个反例, 就可以容易地推翻这个假说。
原始信息——逐一归纳有限的样本具有某种性质————推导出数量有无穷多个的样本也具有某种性质。 归纳只能预测,不能证明。在归纳的基础上,通过演绎证明是不对等的,好比有倒钩的矛头,插入容易,取出难,无损伤取出不可能完成。
三,为什么证明过程不能使用或然推理 数学家在命题证明广泛使用‘估计-多阶估计“”假设-多重假设“,使用归纳法,类比法。使用的”引理“也是论据。 首先,所有的数学定理都是明确的全称判断,明确的意思就是必然判断,而不能是模棱两可的或然判断。 其次,要想结论是必然判断,就必须每一步都是必然判断。必然判断结论只能是演绎推理。 如果前提是或然判断,那么结论必然是或然判断。 估计,多重估计;假设,多重假设都是或然判断。 因为数学是研究数量-空间结构-数量和空间结构的变化,我们面对的情况是复杂的和变化的,常常需要从一个时空到另外一个时空,从一个命题推出另外一个命题,从一个判断中得到另外一个判断。 我们从已知命题推断出未知命题的行为叫推理,已知命题叫前提,未知命题叫结论。我们证明一个结论的系统化行为,叫做论证。 逻辑就是确保这些推理和论证能够有效的规则。逻辑学就是研究这些有效推论和论证规则与标准的学科。 我们借助从老命题引向新的命题-从已知引向未知的。 只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。 而归纳和类比推理不是,逻辑上也不会用有效性与否来评价这两类推理,只会说归纳强度和类比的可接受性。所以也叫或然性推理。 数学定理不能是或然判断。逻辑的本质就是必然得出。演绎推理的前提不能是或然判断的“估计”。 所以,逻辑的合法性来自于形式的合理性,而形式的合理性来自于实践的有效性。溯因达到严格的推理-论证才能叫做定理。 在这里必须是没有任何模糊性,而估计和假设就是模糊证明,结论的正确性建立在前提的正确性和真实性基础上。 归纳假设证明和先验估计命题是数学家常犯的错误: (1)没有进入因果关系; (2)没有进入构成关系; (3)无法被感知。 (4)估计和假设进入证据以后,如果从区分两类否定真理的角度来检视这一问题: 第一类涉及虚构或者主观创造的一些对象; 第二类涉及实际存在的对象。 而估计和假设的虚构的对象并不具有事务的全部属性。 (5)假设最后必须被证明才能进入证据链。 (6),假设理由的虚假性胡乱修改前提条件,得出错误结论。 (7),推理的无关性胡编乱造的结论不能算定理。 (8),隐含的假设性这些结论都有一个共同的缺陷,假设存在他们想要的内容,都是无关地联系他们预想的东西,例如张益唐和陈景润。 (9),论证的单一性这些论证都是违反演绎推理的基本规则,不能反推回去,正确的定理证明,百分之百可以倒推回去。 引理必须用严格演绎法证明1,引理是为证明某个定理或解某个问题所要用到的命题。 引理必须是一个定理,因为引理的逻辑强度必须高于论题,数学家论证某个命题时,还没有直接根据,需要某些还没有被证明的结论,把它提出来加以证明,就是所谓的构造引理。 2,什么叫引理?引理就是在解决某些问题的过程中需要应用一些没有被证明的结论。把它提出来以后必须加以证明,是正确的才能引用。 引理必须被证明--因为它是论据! 论据,也称根据,是在作为论证的命题那个用来确定论题是否真实、并且自身的真实性已经得到断定的或者至少为论证所涉及各方共同接受的命题。 论证之所以必要,就在于论题真假不明显或者尚未得到确定。于是就需要援引论据来判定真假,因此,论据的可信度必须高于论题。如果论据的可信度不高,原有论据对论题的支持关系也就不成立。如果论据是一种假设,最后没有被证明,就是无效论据。 论证与推理的关系,论证总是借助推理进行,论据相当于推理的前提,论题是推理的结论。论证方式反映了论据与论题的关系。任何论证过程都是运用推理的过程,没有推理就无法构成论证。 但是,并非任何推理都是论证。论证总是现有论题,围绕论题寻找论据。这是从结论到前提的过程;而推理是从前提向结论的过度。 论证比推理复杂,构成一个复杂的论证由多个推理完成,是作为一种推理有目的的使用,即证实或者证伪,论证必定要断定论据的真实性和可接受性,否则论证的目的就不能实现。 论证链,各个论据与论题构成整个支持关系必须明确,基本论据是论证中最先引用的无需其他理由支持的论据,一般都是公理或者正确的定理。 主论据与子论据不能互相依赖。 证明过程是线性结构;每一个论据必须环环相扣。 论证过程是发散结构,必须进行收敛证实。 四,论证 1,论证的定义 一种推理形式,它是通过某一种真实的判断,来判断某一个判断的真实性的过程。我们知道判断,这是我们心智对外部世界的肯定,或者否定思维过程。 2,我们判断的依据是什么? 语言或者作为理由的语言,语言必须是清晰的,没有歧义的,符合语法的。语言的正确与否影响我们的判断。判断基本形式,肯定和否定,是一个结果,导致这个结果的理性活动,那个思维基本形式叫做试推,也被译作溯因。试推是我们思维的基本形式。从现实世界到心理世界再到语言世界。 判断是以一个或者多个试推完成的一个结果。 1】,演绎推理,就是从大范畴中找到小范畴的推理;前提与结论是蕴含关系。得出的结论是必然判断。 2】,归纳推理,从众多小范畴中找到大范畴的推理; 3】,类比推理,在相似的范畴之间找到共性的东西和不同的东西。 我们借助从老命题引向新的命题-从已知引向未知的,所谓引理就是一个老命题。 只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。 而归纳和类比推理不是,逻辑上也不会用有效性与否来评价这两类推理,只会说归纳强度和类比的可接受性。所以也叫或然性推理。 数学定理不能是或然判断。数学归纳法产生的不是定理,因为归纳无法产生属性。 命题是什么 命题蕴含了概念和概念的关系,它是词项和连接词组成的事物。表征了外部世间事件的对象,以及对象之间的关系、于是就有了知识,概念是数学的核心。 什么是数学定理
1,数学定理必须是一个明确的判断。 2,数学定理必须是一个全称(一切,所有的,任何,每一个)判断。 3,数学定理是一个已经经过正确的演绎法证明的数学命题(不能使用归纳法和类比法证明,演绎法-三段论有256个格式,只有19个格式有效)。 4,数学定理结构(或者说命题结构)由主项与谓项组成。 5,主项与谓项必须是全异关系(不能是种属关系,例如“庞加莱猜想“就是一个错误的命题,主项与谓项是种属关系;“素数有无穷多个”就是一个正确的命题,因为主项”素数“,与谓项”无穷多个“是全异关系)。 6,主项和谓项的含义必须明确表示和界定,不能有“假设”“估计”。 7,数学定理必须符合语法(例如陶哲轩的”存在任意长的素数算术数列“,主项与谓项都是错误的,主项”素数算术数列”是一个集合概念。谓项“任意长“违反语法:肯定判断谓项不能周延)。 8,用公式表达的定理,每一个符号必须是明确的概念和含义,不能有歧义(例如张益唐的公式)。 9,主项必须是普遍概念或者单独概念,不能是集合概念。 10,数学定理的主项必须经过正确的”种加属差“的方法定义。例如,”素数就是大于1并且只能被1和自身整除的自然数“。 11,一个定理陈述一个给定类所有的元素不变的性质和关系,适用于所有的元素,在任何时候无区别的成立。 五,最后,忠告数学家你们不要徒劳了,人类没有足够的能力证明大多数数学命题。因为,证明数学命题需要正确的语言学知识,需要完整的逻辑学知识,一个人无法在50岁以前学会并且熟练掌握这些知识。再加上数学知识。
|
