3位华人数学家王国祯徐宙利林伟南宣称证明了一种特殊的高维几何拓扑结构,他们使用错误的证明方法:不可靠的归纳法。
如果他们能够构造出来这种结构用于检验,即使没有文字证明,也是可以接受的。
但是,他们所谓证明,本身就是荒唐的猜测与推演,又没有“物质形式”的构造模型,谁会相信呢?
只有演绎法才是可靠的证明。
1,演绎推理,就是从大范畴中找到小范畴的推理;前提与结论是蕴含关系。得出的结论是必然判断。
2,归纳推理,从众多小范畴中找到大范畴的推理;
3,类比推理,在相似的范畴之间找到共性的东西和不同的东西。
A, 只有演绎推理形式是必然有效的,因为大范畴的存在,是小范畴存在的充分条件,所以,演绎推理是必然的因果关系推理。
B, 而归纳和类比推理不是,逻辑上也不会用有效性与否来评价这两类推理,只会说归纳强度和类比的可接受性。所以也叫或然性推理。数学定理不能是或然判断。数学归纳法产生的不是定理,因为归纳无法产生属性。当然可以用归纳法进行评价问题。
问题:
将三维空间中的直觉照搬到高维王国里看上去很诱人。毕竟,添加又一个维度只是长出了一个新的方向,可以在其中盘桓。这并不改变空间的定义性质:无边性与均匀性。
但不同的维度有着截然不同的个性。在8维和24维里,可以将球异常紧密地堆积在一起。在其它维 度里,存在“奇异”的球,它们看上去皱得不可救药。而维度3是唯一能容纳扭结的——在任何更高的维度,哪怕你把结的末端牢牢地固定住,也可以把它解开。
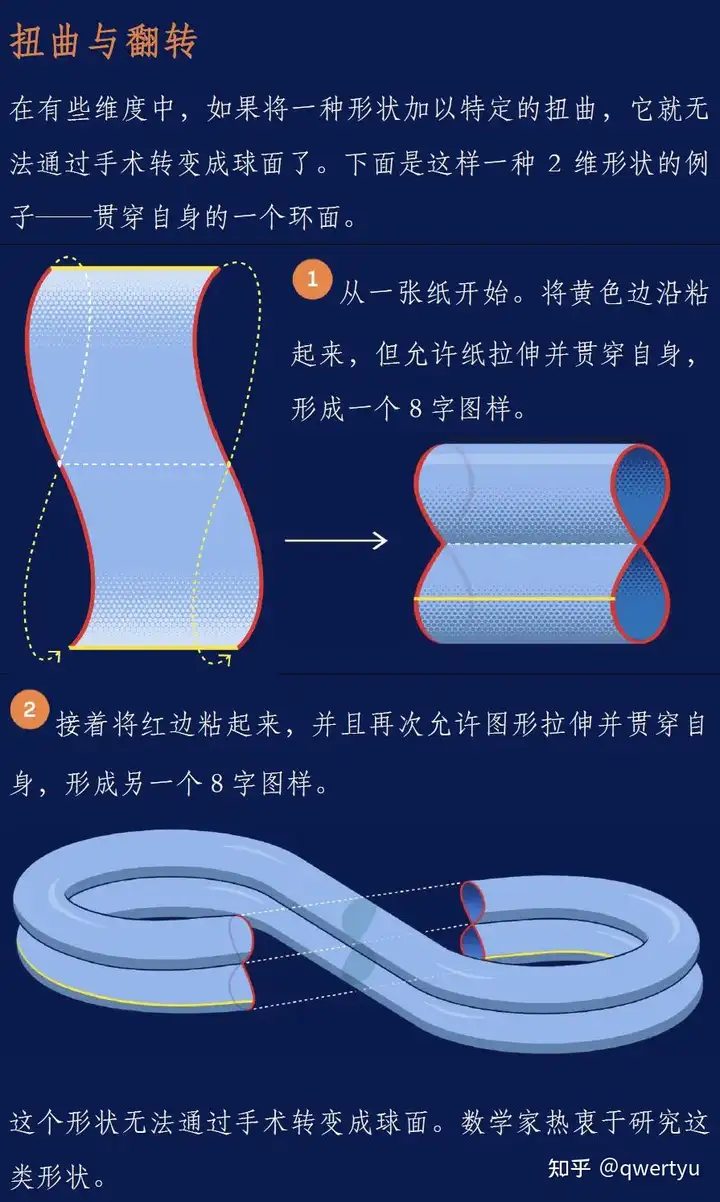
如今,在一个诞生至今已经65年之久的维度怪异性故事上,数学家们终于迎来了结局。数十年来,研究者们一直想知晓哪些维度可以容纳某种特定的奇怪形状——它们极度扭曲以致无法通过一个被称为“手术”的简单过程转变成球面。数学家们已经证明,这些形状的存在与拓扑学中不同维度球面之间的关系这种基本问题紧密纠缠在一起。
经过这些年,数学家发现这种扭曲形状在2,6,14,30和62维中存在。他们还证明这类形状不可能在任何其它维度中存在——但有一个例外。没人能确定126维的状况。
三位数学家宣称解决了这一遗留问题。在去年12月在线公布的一篇文章中,复旦大学的林伟南、王国祯与加州大学洛杉矶分校的徐宙利证明126其实也是能容纳这些奇特扭曲形状的几个罕见维度之一。
他们不是通过演绎方法证明,而是归纳法证明,
尽管新文章证明了126维存在奇特的扭曲形状,
它并没有给出构造它们的思路。
研究者们已经在前面四个特定Kervaire维度2,6,14和30中都找到了特殊的扭曲形状。
不过还没人在62或126维中找到一个,哪怕在这些形状存在的任意一个维度里,它们都占据了所有可能形状中的整整一半。
几何构造比代数构造少,并且,几何构造困难的多。人类至今没有一个4维和4维以上的几何构造坐标,因为4维构造破坏了3维坐标中——长-宽-高坐标两两相连90度架构。你增加一个维度,就会压缩3维坐标的90度结构,这个问题没有解决,126维的歧管是一个什么怪物?
况且,三位数学家归纳证明还使用错误的反证法,用假设否定假设。不过是一个闹剧而已。
详见论文截图:使用归纳法证明。荒唐吧?







编
|
