我审查了丘成桐的全部数学证明论文,无一例外地都是错误的。例如对卡拉比猜想的证明。 数学白痴丘成桐说:
1,卡拉比猜想实际上与蒙日-安培方程等价。
2,他花了将近3年时间,做了大量准备工作,在1976年6月求解了这个非线性复蒙日-安培方程(至多有一个解)。
参见维基百科卡拉比猜想; 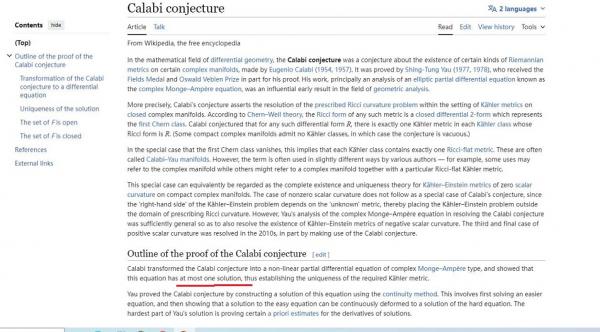
3,从而给出了卡拉比猜想的证明(实际上是:丘成桐证明了其流形上复数的蒙日—安培方程,至多只有一个解。
丘成桐说的【至多有一个解】的含义是:
1,否定至少有两个或者两个以上的解,最多一个解(上限)。
2,不能保证有一个解。很可能一个解也没有(下限)。
就是说,如果没有一个解的情况下,就不能说丘成桐解开了蒙日-安培方程。
为什么?因为,【至多只有一个解】属于或然性推理。或然性推理的前提与结论之间没有蕴含关系,所以,数学定理必须是必然判断。 丘成桐思维混乱,智力低下。 丘成桐简化证明,引用陈省身和小平邦彦的错误论文
在摘要中:摘要我们证明了卡拉比关于紧致凯勒流形里奇曲率猜想的理论依据,.....。建立了此类度量的唯一性,并在假设Rij接近Ri时证明了其存在性。无需对M或Rij作任何假设,仅存在z Rij dziI dii的性质被称为卡拉比猜想。 (注意,在假设时证明了存在性,这是预期理由的逻辑错误,而卡拉比猜想要求是没有任何假设情况下证明,就是说,丘成桐没有证明卡拉比猜想,丘成桐的老师陈省身证明高斯-博内定理也是在假设下的预期理由错误)


丘成桐引用陈省身的错误论文-归纳法证明




小平邦彦的归纳法证明 
陈省身证明高斯-博内公式也是在假设下: 

|
