物理,揭开了和声的神秘面纱
Ming Cheng
前几天写了一篇 蒙古呼麦, 泛音和物理, 解释了蒙古呼麦的奥秘 现在,论坛上在争论和声,似乎神秘莫测. 我们再来看看这篇文章。里面说到,我们在物理上知道,任何一个声音,或者是波形,在物理上通过傅立叶变换,可以分解成一系列的正弦波的叠加。频率最低的那个正弦波叫做“基波”,而频率较高的各个正弦波叫做“谐波”。谐波的频率为基波的两倍的叫做“二次谐波”,可以依次类推,所谓 high harmonics,如下图所示。在声乐中也称为泛音或泛音列。 。
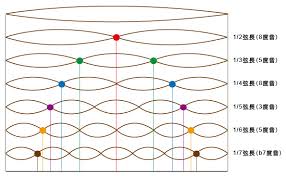
我们用泛音列解释了蒙古呼麦,今天我们又要用到它来解释和声。 其实,学科学的很容易从这里想到,既然一个声音可以分解为泛音列,那么按泛音列排列的多个声音也应该可以合成一个声音。Bingo! 这就是和声的来源,或者说和声的物理基础。即使他们不满足成为一个音的条件,如相位和单频等等,但它们之间显然比其他组音更具有和谐关系。其实如果完全成为一个音反而没有什么意义了,就如八度音一样,它就是它自己。
我们看到,泛音列之间的泛音的频率比都成简单的整数比。
2:1, 在音乐上我们称为八度 以下类推 3:2, 五度 4:3, 四度 5:4, 大三度 6:5, 小三度
三个音的频率比,如著名的大三和弦是一个“大三度”再叠置一个“小三度”共三个音的频率比是 4:5 :6。如果我们继续往下推,可以得出小三和弦的三个频率比是10∶12∶15,所以它们的和谐度不如大三和弦。对比这两组数,会发现在数学上有很强的相似性,但和声的实质其实在后面的物理。
当然,这只是和声理论的来源和基础。奠定现代和声理论基础的拉莫的和声理论的第一条就是: 和弦以泛音列为基础,
至于和声理论的其他部分,其实也离不开其物理基础。但一般音乐学院不教这些。毕竟你不忍心在音乐学院对那些漂亮的小姑娘教授物理,而把它们抽象为音乐理论。多数音乐学生对这些都是死记硬背. 比如说, 为什么和弦以三度构建, 当然有调式上的理由,三度可以帮助确定调式,但后面也有更深刻的物理。我们下次分别再谈. |
