生成模型中的素数分布:AI视角的几何学习1. 训练目标与数据构造我们将素数间隔序列构造为高维向量: vn=(pn+1−pn, pn+2−pn+1,…,pn+k−pn+k−1)∈Rkv_n = (p_{n+1}-p_n,\ p_{n+2}-p_{n+1},\dots,p_{n+k}-p_{n+k-1}) \in \mathbb{R}^k 这些向量形成点云,具有高度非线性但低维嵌入特性。 多尺度几何结构: 小尺度下,孪生素数、三生素数形成局部簇;大尺度下,素数定理的渐近规律占主导。生成模型必须具备多尺度捕捉能力,可通过小波变换提取特征并作为条件输入。 2. 模型设计与几何约束主成分对齐损失LPCA=∑i=1d(1−cos∠(u^i, ui))\mathcal{L}_{\mathrm{PCA}}=\sum_{i=1}^d \Big(1-\cos\angle(\hat u_i,\ u_i)\Big) 保证生成数据与真实数据的主子空间一致。 拓扑保持项LTopo=dbottleneck(D(V^),D(V))\mathcal{L}_{\mathrm{Topo}}=d_{\mathrm{bottleneck}}(D(\hat V),D(V)) 保持持久同调的全局形状。 对称性与不变性间隔分布在缩放、旋转、局部置换下近似不变。设计等变网络嵌入这些先验,提高泛化能力。 算术簇条件化欧拉多项式与算术级数生成的素数形成特定簇,可作为条件标签指导模型学习。 综合损失: L=Lgen+λPCALPCA+λTopoLTopo+λsymLsym+λcondLcond\mathcal{L}=\mathcal{L}_{\mathrm{gen}}+\lambda_{\mathrm{PCA}}\mathcal{L}_{\mathrm{PCA}}+\lambda_{\mathrm{Topo}}\mathcal{L}_{\mathrm{Topo}}+\lambda_{\mathrm{sym}}\mathcal{L}_{\mathrm{sym}}+\lambda_{\mathrm{cond}}\mathcal{L}_{\mathrm{cond}} 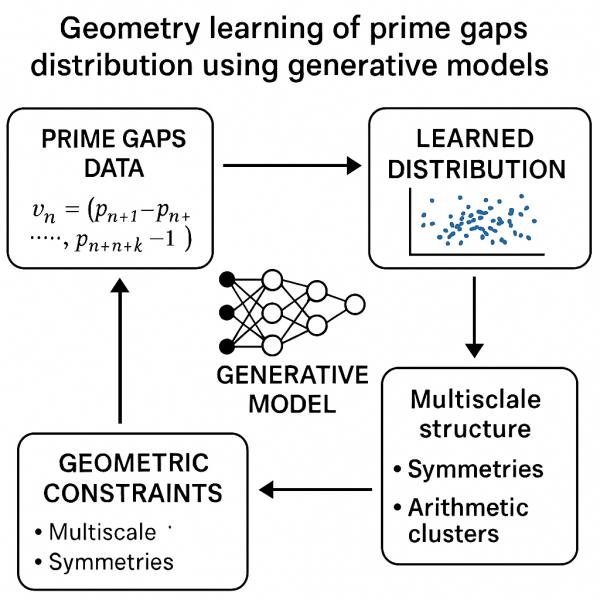
图注: AI生成模型学习素数间隔分布的几何结构流程图。图中展示了从原始素数间隔数据构造(左上),通过神经网络模型进行生成(中间),得到学习后的分布(右上),并通过几何约束(下方)如多尺度结构、对称性与算术簇反馈优化模型。整个过程形成一个闭环,体现了数据驱动与结构约束协同作用于素数几何学习的机制。 3. 已有实验结果Kolpakov & Rocke (2024, PLOS ONE)GPAI 团队 (2025)生成模型实验(GAN/扩散)能在高维间隔空间中重建低维嵌入结构。 结果主要是拟合已知规律,而非发现新规律。
局限性总结: 4. 改进方法与未来方向多尺度条件化:显式引入小波特征,使模型同时学习局部簇与全局趋势。 等变网络结构:融入旋转、缩放不变性,提高模型对几何对称性的捕捉能力。 算术簇标签:将二次多项式簇、算术级数簇作为条件信息,提升模型对特定模式的学习。 潜空间解释性:使用 β-VAE 或 InfoGAN,促进潜因子解缠,建立潜空间轴与算术性质的对应。 跨领域比较:将素数间隔生成模型与随机矩阵理论、混沌系统的生成模型对比,寻找更深层联系。 开源与基准化:建立公开基准集,比较不同模型的几何—拓扑表现,促进可重复性。
5.结语(增强版)已有实验表明,AI生成模型确实能够学习素数分布的统计规律与几何特征,重现如素数定理、孪生素数簇、间隔分布的正态近似等经典现象,并在高维间隔空间中构建出与真实数据相似的低维嵌入结构。这些成果验证了素数分布的“可学习性”,也证明了几何视角在数论中的解释力。然而,迄今为止,AI尚未发现新的定理或提出可验证的数论猜想,其潜空间结构与深层算术对象(如黎曼ζ函数零点、模空间上的轨迹)之间的联系仍属未知。 要使AI从“验证工具”跃升为“猜想生成者”,我们提出以下具体改进设想: 1. 多尺度几何分析的深度融合将小波变换、尺度空间理论与生成模型结构结合,使模型在不同尺度上分别学习局部簇(如孪生素数)与全局趋势(如素数定理)。在训练中引入多尺度损失项,分别对不同频带的几何结构进行约束,并在潜空间中建立尺度因子与几何簇之间的映射。 2. 对称性与不变性嵌入的结构化实现设计具备旋转、缩放、置换等群等变性的生成网络(如E(2)-等变卷积、置换等变Transformer),使模型在几何变换下保持结构稳定性。通过对称性约束损失项,强化模型对素数分布中隐含对称结构的识别能力,提升泛化性与解释性。 3. 算术簇的条件生成与分层建模将已知生成素数的算术机制(如欧拉多项式、狄利克雷同余类)作为标签嵌入模型,使其在不同簇上分别学习几何风格。进一步构建“簇内几何保持 + 簇间几何分离”的对比损失,使模型在生成时能区分不同算术来源的结构,并在潜空间中形成可解释的簇分布。 4. 潜空间的语义解缠与因子映射使用 β-VAE、InfoGAN 等结构促进潜因子的解缠,使每个潜变量对应一个几何或算术特征(如平均间隔、周期性、簇标签)。通过线性探针与非线性回归,将潜空间轴与素数簇、模空间轨迹、ζ函数零点频率等数学对象建立映射关系,探索“潜空间—数论结构”的桥梁。 5. 跨领域结构对比与谱几何分析将生成模型中学到的几何结构与其他数学领域(如随机矩阵理论、量子混沌、动力系统)中的谱结构进行对比,寻找素数分布与酉群特征值、能级间隔、重正化群不动点之间的几何对应。通过谱统计与拓扑不变量的比较,构建跨领域的结构类比与猜想生成机制。 6. 开源实验平台与可验证猜想生成建立开放的素数几何生成平台,提供标准数据集、模型结构、评估指标与可视化工具,鼓励研究者在不同簇、不同尺度、不同模型下生成数据并提出猜想。通过自动化的几何—算术分析模块,将生成数据中的规律转化为可验证的数论猜想,并与已有理论进行对比与归纳。 综上所述,AI生成模型在素数分布研究中的角色正在从“拟合者”向“结构发现者”转变。通过引入多尺度分析、对称性嵌入、算术簇条件化、潜空间解释性与跨领域结构对比,我们不仅可以提升模型的几何保形能力,更可能在潜空间中发现隐藏的数论结构,从而提出新的猜想。这一方向不仅是数论的实验工具,更是未来数学发现的启发源泉。它代表着一种新的研究范式:用几何与信息的语言,去探索整数的深层逻辑与宇宙的对称性。
|
