戴榕菁 这两天发现了作为刚体动力学的基础方程的欧拉方程在推导中存在一个意想不到的错误。虽然那是刚体动力学的基本方程,但是那个错误基本上属于一个数学错误。所以正如本文标题所示,尽管我相当肯定发现了一个错误,但仍不敢相信这是真的。。。。那可是欧拉呀。。。。这一方面是因为以欧拉的名头,如果有任何人出来说找到了欧拉的一个数学错误,那可比推翻相对论和康托的集合论更让人难以置信;另一方面因为这里出问题的既不是象相对论那种无法用实验验证的数学模型也不是在量子力学那种看不见摸不着的领域,而是在过去几百年里被无数位教师和科学及工程人员应用并验证了刚体动力学的基础方程。。。。 好了,还是先把我发现的问题介绍一下,然后读者们可以一起公论看我是否错怪了欧拉大师。 我所发现的是作为刚体动力学的基础之欧拉方程(Euler’s Equations of Rigid Body Dynamics)在推导过程中的一个错误导致了其结果的错误。欧拉方程推导的出发点是角动量守恒定律,假设惯性系中有一个刚体B,我们有: 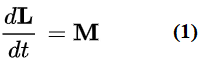
其中L为角动量,M为外力矩,t是时间。根据转动力学我们有:
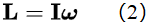
其中I是刚体B在惯性系中的转动惯量矩阵,ω是B在惯性系中的角速度。假设我们有一个旋转坐标系R,其在惯性系中的角速度为Ω,那么我们有:
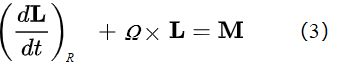
(3)式中的下标R表示是在旋转坐标系R中对时间求导。将(2)代入(3),我们有
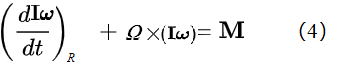
(4)式又可表达为:
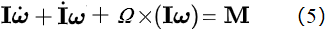
其中İ是刚体B的转动惯量矩阵在R中对时间求导数,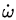 是B的角速度在R中对时间求导。 是B的角速度在R中对时间求导。 现在将坐标系R固定在刚体B上,这时因为刚体B随着R一起转动,所以İ = 0, 因此我们有:
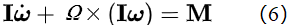
但另一方面,当刚体B随着R一起转动时,我们有Ω = ω,所以(6)变为:
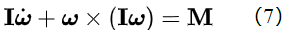
(7)就是著名的欧拉方程【[1]】。这个公式据说是欧拉在1736年发表的,但可惜的是我目前还没有找到欧拉的原文的英文翻译。 相信这里的绝大多数读者到这一步为止和过去几百年里的所有学者一样并没有看出上面的推导有什么问题。 下面我们稍改变一下推导步骤,我们不要等到方程(6)才令Ω = ω,而是在(3)中就令Ω = ω,这样我们便有下面这个方程: 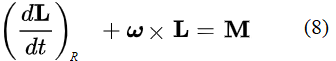
到这一步,我猜很多读者应该看出问题了吧!没错,(8)式中的第二项应该等于0!这是因为其中的ω//L,而两个平行矢量的叉积为零! 因此我们根本不应该有(7)式,而应该有: 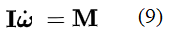
不要以为(9)式只是(7)式当第二项为零时的特例。完全不是。当人们用(7)式来解题时,得出的结果完全可以不满足第二项等于零这个条件!也就是说(7)式根本就是一个错误的公式因为只要其第二项不等于零就打破角动量守恒而欧拉方程的出发点就角动量守恒! 结论: 作为刚体动力学的基本方程的大名鼎鼎的欧拉方程(7)是错的!!! 我相信凡是对刚体动力学有些了解的读者或对欧拉如雷贯耳的大名有所耳闻的读者看到上面这个结论后都会感到难以置信。写到这里我不得不再重复一下本文的标题:欧拉会犯这样的错误吗? 这个错误看上去也太简单了些吧?欧拉是谁呀?假如今天要问在用人名命名的定理,公式,方程,甚至方法中谁的名字被用得最多的,那么我想欧拉是当之无愧的了。你在网上查“欧拉定理”或“欧拉公式”的话,会大概率地得到不是你要的结果,因为以欧拉命名的定理和公式太多了。不仅如此,有些不是用他名字命名的都和他脱不了干系。比如被拿来当作现代物理学最最基础的“作用”虽然是莫佩尔蒂(Maupertuis)最先提出的,莫佩尔蒂却因为提出“作用”这个概念被学界耻笑而喊冤离世,后来是欧拉认可了“作用”这个概念,才使得整个学界采用了“作用”这个概念的。 这么一位过去几百年里的学界泰斗会犯这么简单的错误?这确实是一个让我有些诚惶诚恐的问题。 但另一方面,如果有谁站出来说欧拉没错,那他还真得要拿出真格的来告诉我在上面的分析中我错在哪里了! 尴尬: 如果说发现欧拉方程出错会让我感到诚惶诚恐的话,那么接下来的问题就让我极其尴尬了: 在找到欧拉方程的推导过程中的错误之后,我居然无法确定到底是哪一步导致了那个错误! 虽然从上面的讨论来看,导致方程(7)出错的直接原因似乎是令Ω = ω这一步,但这一步本身是没有问题的呀!凭什么不能令Ω = ω呢? 如果不是令Ω = ω导致(7)出错的话,那么只能是由(1)得出(3)这一步了。但是,这一步也是过去几百年里人们一致认可的经典操作呀! 这么看来,欧拉大师所犯的错误虽然乍看起来是中学生都能看出来的没有令两个平行的矢量等于零这么一个简单的错误,但其背后的原因并没有看起来那么简单------这恐怕就是为什么欧拉大师会犯下那样的错误,而之后几百年里的无数学者和工程人员又都没有发现那个错误的原因!
可以说,欧拉推导的每一步按照我们现在已知的知识标准来说都没有错,但却得出了一个明显错误的结果!这可能是这个问题最有趣也是最可怕之处 ---- 这意味着现有的知识体系一定存在着我们目前来说还搞不清的严重隐患! 讨论: 我相信读到这里最让读者们不可思议的还是:过去几百年里包括航天卫星航空飞机以及各种机械工程在内的无数次实际设计中都会用到刚体力学的欧拉方程,大学教学课堂上不但会讲到刚体力学的欧拉方程还大概率地会将刚体力学的欧拉方程用在数值模拟中来解决具体问题。难道这过程中都没有人会发现刚体力学的欧拉方程其实是有问题的吗? 对于这个问题我的看法是:在现实设计或模拟计算中,(7)式的第二项虽然可以(错误地)不是零,但是与右边的外力矩M相比通常可能是一个较小的值,因此通常可能都落在了工程设计或数值模拟的误差范围之内,所以一直能安然地混过了将近3百年。 而我这次之所以会发现这个问题是因为我要破解的是M=0的情况。对了,就是那个贾尼别科夫效应的问题。自从1985年贾尼别科夫发现了那个效应之后,主流学界都沿用法国数学家和力学家Louis Poinsot在1834年研究中轴定理时用的方法,而Louis Poinsot也不是一个普通人物。但他虽然是在M=0的前提下(不知为什么在没有人造卫星的年代他会对那个前提感兴趣)用欧拉方程进行的分析,却也没能看出欧拉大师所犯的那个错误。 而我之所以会追究欧拉方程所存在的问题并不仅是因为我从视频上看到了贾尼别科夫效应打破了角动量守恒定律,而更主要的是因为当代的主流学界用欧拉方程分析贾尼别科夫效应时明显得出打破角动量守恒的结果但他们却出现了集体近视,所有的人都好像没有看到这一点。科普网红们【[2]】更是津津乐道地用主流学界从Louis Poinsot学来的稳定性分析来解释贾尼别科夫效应,就好像他们的结果完全没有打破任何定律似的。 既然他们用欧拉方程对贾尼别科夫效应进行的所谓稳定性分析的结果明显打破角动量守恒,而他们又都或是集体近视或是集体假装没看见,我就只有再一如既往地在上帝的带领下,如同过去几年里推翻各种被物理学界或数学界权威们认作不可触犯的金科玉律的理论时做过的一样,一步步地细究为什么从角动量守恒出发的欧拉方程会得出打破角动量守恒的结果呢? 细究的结果发现是欧拉方程(即上面的(7)式)中的第二项原本不应该出现,而当外力矩等于零的时候,那一项就相当于给运动物体额外加了一个外力矩【[3]】。 结束语 在上帝的带领下,经过一个多月的努力【3,[4],[5],[6],[7]】,对于贾尼别科夫效应我提出了如下三个悖论: 1)人们按照Louis Poinsot的中间轴定理之证明逻辑对贾尼别科夫效应进行的所谓的稳定性分析可以在I1 <I2 < I3的前提下得出绕中间轴旋转时会出现他们称之为不稳定状况的结论,而该结论与实验观察大体一致;但是运用该逻辑却完全无法预测I2 < I1 = I3 或I2 > I1 = I3条件下物体的贾尼别科夫效应。 2)在对于贾尼别科夫效应的所谓稳定性分析中,人们通过由角动量守恒推导出的欧拉方程得出了实际上打破角动量守恒的结果; 3)贾尼别科夫效应打破了过去几百年里作为物理学最基本的角动量守恒定律(也就是打破了牛顿第二定律)。 本文及本人这两天贴出的英文文章【3】给出了导致上面第二个悖论的原因。
知道了本文给出的导致第二个悖论的原因之后我们就比较容易解释第一个悖论了:如前所述,当外力矩M为零时,(7)式中本应为零但却因为欧拉的错误而没有被置零的那项(即第二项)就人为地为物体的运动提供了一个虚构的外力矩,其表达形式如下: 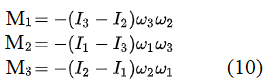
将(10)代入(7)中并令其中的M = 0,我们便得到主流学界对贾尼别科夫效应进行稳定性分析的出发方程:
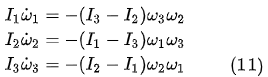
由这个方程进行所谓的稳定性分析就会得出Louis Poinssot的中间轴定理以及当今主流学界对贾尼别科夫效应进行分析的结果。所以,第一个悖论其实是由(7)式的错误凑巧得出在特定前提下的“正确”结果。 而上面三个悖论中真正最具震撼性的还是第3个悖论:贾尼别科夫效应打破了过去几百年里作为物理学最基本的角动量守恒定律。 不仅如此,贾尼别科夫效应在打破角动量守恒的同时也打破了能量守恒,这也坐实了自2021年以来我所指出的能量并非总是守恒的这一论断【[8]】。
[[1]]Wikipedia. Euler's equations (rigid body dynamics). Retrieved from: https://en.wikipedia.org/wiki/Euler%27s_equations_(rigid_body_dynamics). Last edited on 22 February 2025, at 23:52 (UTC). 【[2]】李永乐(2022)南北极翻转地球毁灭?贾尼别科夫效应最硬核解释!url:https://www.youtube.com/watch?v=ASzflQV-WXE. [[3]]Dai, R. (2025). Dzhanibekov Effect --- A Smashing Challenge to the Foundation of Physics. Retrieved from: https://www.researchgate.net/publication/390097038_Dzhanibekov_Effect_---A_Smashing_Challenge_to_the_Foundation_of_Physics 【[4]】戴榕菁 (2025)一个打脸中间轴定理证明的例子 【[5]】戴榕菁 (2025)那就来聊聊数学 【[6]】戴榕菁 (2025)再聊聊贾尼别科夫效应 【[7]】戴榕菁 (2025)难道被苏联封了40年的真正秘密是。。。? [[8]] Dai, R. (2024). When Philosophy is Disparaged. Scholars’ Press. ISBN: 978-620-6-77202-6. 
|
