戴榕菁 1.背景 前文“那就來聊聊數學”【[1]】中指出對太空站中的賈尼別科夫效應進行所謂的穩定性分析的人所採取的是據說將近兩百年前法國數學家和物理學家Louis Poinsot的方法,其出發點是外力矩為零的剛體運動歐拉方程【[2]】: 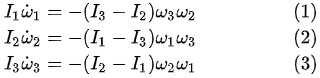
其中I1,I2,I3是物體的主慣性矩且被假設為 I1 < I2 < I3 ω1,ω2,ω3是沿着三個主軸方向的角速度分量,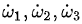 是三個主軸方向的角加速度分量。 是三個主軸方向的角加速度分量。 我在那篇文章中只討論了與賈尼別科夫效應有關的情況,也就是旋轉物體發生翻轉的情況。為了打臉他們的證明,這裡我們來完整地看一下他們的證明。首先,他們考慮繞最小慣量軸的轉動。他們在上面方程組的(2) 式中對時間求導,因為在繞最小慣量軸的轉動中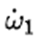 很小,所以忽略掉結果中的 很小,所以忽略掉結果中的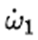 項,然後將(3)式中的 項,然後將(3)式中的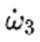 代入求導的結果從而得到: 代入求導的結果從而得到: 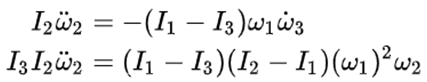 (4) (4)
因為I1 < I2 < I3,所以(I1 – I3)( I2 - I1) < 0,所以 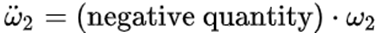
由此他們得出結論說,(因為 與 與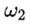 符號相反) 符號相反)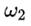 會得到抑制。用白話解釋,就是說假如 會得到抑制。用白話解釋,就是說假如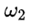 是正的,那麼沿着 是正的,那麼沿着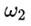 的方向的角加速度 的方向的角加速度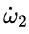 就會在那個方向上減小,如果 就會在那個方向上減小,如果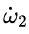 一開始為零,那麼就會出現一個負的 一開始為零,那麼就會出現一個負的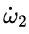 使得 使得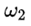 變得越來越小。當 變得越來越小。當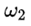 變為0時, 變為0時, 為零,此時 為零,此時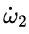 將繼續保持負的從而產生反向的 將繼續保持負的從而產生反向的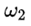 ,但這時反向的 ,但這時反向的 也將產生,使得負 也將產生,使得負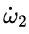 開始變小,反向的 開始變小,反向的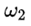 繼續增大直到 繼續增大直到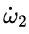 降為零,然後反向的 降為零,然後反向的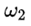 又開始變小。。。。 又開始變小。。。。 他們認為這樣的運動是穩定的。並且,他們說這一結論也適用於繞最大慣量軸的旋轉,所以在太空站中的物體繞最大和最小慣量軸的旋轉是穩定的。 然後他們將上面方程組的(1)式對時間求導,因為在繞中間慣量軸的轉動中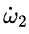 很小,所以忽略掉結果中的 很小,所以忽略掉結果中的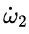 項,並將(3)式中的 項,並將(3)式中的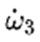 代入求導的結果從而得到: 代入求導的結果從而得到: 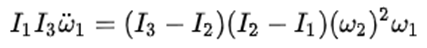 (5) (5)
因為I1 < I2 < I3,所以(I3 - I2)( I2 - I1) > 0,所以 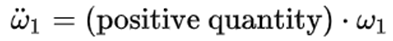
由此他們得出結論說,只要一開始的時候ω1有一個非常小的值,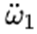 就有一個大於零的值,也就是說 就有一個大於零的值,也就是說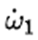 會越來越大,所以運動是不穩定的從而會出現翻轉。 會越來越大,所以運動是不穩定的從而會出現翻轉。 上面這套論述就是現有的據說是來自近兩百年前的Louis Poinsot的證明所謂的中間軸定理的內容。 2.打臉現有的穩定性分析 現在我來考慮這樣的條件:I2 < I1 = I3 或I2 > I1 = I3,這樣一來(4)的右邊等於零,因此如果一開始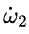 為零的話,它仍然可以永遠為零,按照他們的邏輯,這時繞軸1和軸3的旋轉應該仍然是穩定的;但是,這時(5)的正負號就要顛倒了,也就是說這時我們不再有 為零的話,它仍然可以永遠為零,按照他們的邏輯,這時繞軸1和軸3的旋轉應該仍然是穩定的;但是,這時(5)的正負號就要顛倒了,也就是說這時我們不再有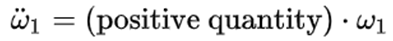 而是會有: 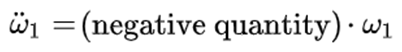
這樣一來,按照他們的邏輯這時繞2軸的旋轉也將是穩定的了。但下面這個視頻中的圓盤上的所有轉動慣量都是相等的,所以滿足I2 < I1 = I3 或I2 > I1 = I3的條件。該視頻告訴我們繞2軸的旋轉顯然是不穩定的,從而否定了上述的自Poinsot以來的關於中間軸定理的證明邏輯: https://www.youtube.com/watch?v=Xrf1HzFJ8jc&t=39s 3.結論 上面的例子告訴我們自1834年以來人們對於中間軸定理的分析邏輯是錯的!我之所以說他們的邏輯錯了,是因為按照他們的邏輯會得出與實驗結果相反的結論。 這裡要特別指出本文所討論的I2 < I1 = I3 或I2 > I1 = I3條件下的物體的賈尼別科夫效應之重要性在於它在不需要涉及如何用歐拉方程具體描述翻轉過程中角動量是如何被打破的前提下,用自1834年以來人們針對所謂的中間軸定理的穩定性分析方法本身否定了其邏輯的可靠性。可以說是以子之矛攻子之盾,從而它給了那些認為現有的穩定性分析足以解釋賈尼別科夫效應的論調(如李網紅的視頻【[3]】)致命的一擊:如果你的解釋本身的邏輯都經不住實驗的檢驗,你憑什麼認為你的說辭就足以解釋賈尼別科夫效應了呢? 綜合過去一個多月來本博客關於賈尼別科夫效應的討論【1,[4],[5]】,我們現在可以做出如下幾個結論: 1)賈尼別科夫效應打破了過去幾百年裡作為物理學最基本的角動量守恆定律(也就是打破了牛頓第二定律); 2)在Louis Poinsot的方法中,人們通過由角動量守恆推導出的歐拉方程得出了實際上打破角動量守恆的結果; 3)空間站中符合I2 < I1 = I3 或I2 > I1 = I3條件的物體的賈尼別科夫效應表明人們按照Louis Poinsot的方法對所謂的中間軸定理的證明邏輯中存在缺陷。 4. 討論 但另一方面,不可否認的是,按照他們的邏輯也確實得出了在I1 < I2 < I3的前提下繞2軸的運動會與繞1軸和3軸的運動不同這一結論,只不過如我在“那就來聊聊數學”【1】一文中指出的,他們的這一結論本身又有着很大的瑕疵:他們由於未能描述翻轉的運動過程而似乎暗示物體在開始翻轉之後就無法用歐拉方程來描述了,而無法用歐拉方程描述這一點本身又意味着違背角動量守恆,但他們的分析顯然無法解釋正確為什麼角動量守恆會被打破。 這裡我們面對着這樣幾個問題: 1)為什麼會出現角動量明顯不守恆的現象? 2)為什麼由Pointsot簡化了的歐拉方程會得出角動量不守恆的結果? 3)為什麼明明Pointsot的證明邏輯錯了,還能正確地指出在I1 < I2 < I3的前提下繞2軸的運動會與繞1軸和3軸的運動不同這一結論? 這是三個不同層次的問題,彼此之間既可能相互關聯也不一定就有着必然的聯繫。 假如從角動量守恆出發的歐拉方程的推導或Pointsot對歐拉方程的運用中存在問題,那麼上面的第一個和第二個問題就是兩個完全不同性質的問題。。。。但是,如果歐拉方程的推導沒有問題而且Pointsot對歐拉方程運用也沒有問題的話,那麼上面的第一個和第二個問題就是兩個彼此關聯的問題了。 至於說第三個問題,顯然與前兩個問題的性質不同。首先,儘管實驗的結果表明他們用來得出中間軸定理之結論的邏輯明顯不成立,但那只是對於數學結果的解釋上出了問題,而並不等於說他們的數學推導本身有問題。第二,至於說為什麼用被實驗證明錯誤的邏輯可以得出在一定程度上正確的結果這一點,一個簡單的答案是碰巧了,但也可能真正的原因並不那麼簡單,而是與前面兩個問題象關聯。 。。。。 過去這些年曾有網友在我的文章後面問我要如何進行形而上的分析。我這裡列出三個問題這種做法就是比較典型的形而上的分析形式。。。。這裡涉及到的邏輯其實相當複雜,而通過形而上的分析可以把這裡所涉及到的複雜邏輯整理清楚,這樣可以便於日後的進一步研究分析。 5. 結束語 在過去一個多月里關注了我對於賈尼別科夫效應的討論的讀者在看完上面那個視頻後可能已經發現我在之前的文章中已多次用到該視頻,因而可能會產生這樣的疑問:為什麼我之前沒有看出該視頻實際打臉自1834年以來對於所謂的中間軸定理的證明邏輯呢? 這裡的答案其實既有點辛酸也很特別但也伴隨着屬靈的喜樂。。。。其特別的程度已經達到我無法解釋的程度,有多特別呢?答案是:如果不是我親身經歷,任誰和我說,我也不會相信會有這樣的事情發生。。。。鑑於此,我就無法用簡單的語言在這裡描述過去幾個月發生在我身的“怪”事了。。。。當然,更重要的是:上帝一直在保護我,使得我未被擊垮,而且我堅信上帝會救我脫離目前的危險處境! 不過過去這幾個月的艱辛確實在一定程度上影響了我的哲學閱讀,調研和寫作。但與此同時,感謝上帝的看顧和帶領,我的靈命則在大大成長。我相信看到在那樣的持續重擊之下我不但能挺到現在並身體保持基本健康而且靈命不斷成長,氣得哇哇叫的是魔鬼! 感謝上帝!一切榮耀歸於上帝!
【[1]】戴榕菁 (2025)那就來聊聊數學 [[2]] Wikipedia. Tennis racket theorem. Retrieved from: https://en.wikipedia.org/wiki/Tennis_racket_theorem. Last edited on 29 November 2024, at 06:27 (UTC).
【[3]】李永樂(2022)南北極翻轉地球毀滅?賈尼別科夫效應最硬核解釋!url:https://www.youtube.com/watch?v=ASzflQV-WXE. 【[4]】戴榕菁 (2025)再聊聊賈尼別科夫效應 【[5]】戴榕菁 (2025)難道被蘇聯封了40年的真正秘密是。。。?

|
