第十二章：洛伦茨的迷惑

李四洋洋灑灑地高谈阔论了一番，张三笑起来了，说李四犯了和他的物理界老祖宗们一样的毛病，把物理当成哲学了。物理毕竟不是哲学，你还是给我们讲一些具體点的东西吧，讲與你的那个X教授做的课题有点关系的。

李四扶正了带着的深度近视眼镜，仍然不紧不慢的，一边打开一本书，一边说，这不马上就要进到正题了吗∶经典力学为何导出了决定论? 混沌理论又是怎样证明一个决定论的系统也可以出现随機的行为的呢? 你们看，当我们翻开任何一本关於混沌数学的书, 差不多都能看到與图（12.1）类似的图案。那是混沌理论的著名标签∶‘洛伦茨吸引子’:

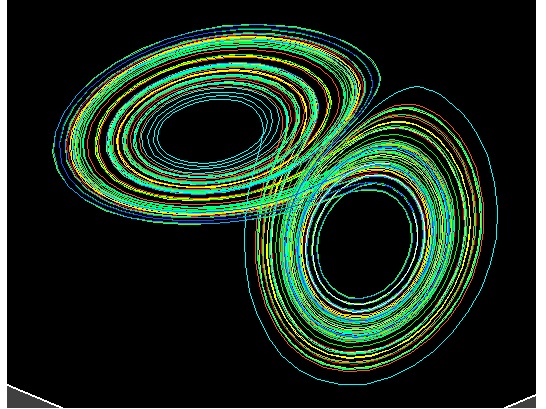图（12.1）∶洛伦茨吸引子

点击此图到JAVA演示程序

“什厶是‘吸引子’啊？”王二问。

李四摸了摸大脑袋说∶“你的问题提得好啊，不过，‘吸引子’这个题目超前了一点兒，以後再讲。今天，我先讲讲这个图的来由，讲讲洛伦茨的工作吧┅┅”

爱德华·洛伦茨（1917-2008）是一位在美国麻省理工学院做氣象研究的科学家。上世纪的60年代初, 他试图用计算機来模拟影响氣象的大氣流。当时，他用的还是由真空管组成的计算機，那是一个充满整间实验室的庞然大物啊。我想，那機器虽然大，计算速度还远不及我们现在用的这些电脑吧。所以，可想而知，洛伦茨没日没夜的，工作得很辛苦。严谨的科学家不放心只算了一次的结果, 决定再作一次计算。为了节约一些时间, 他对计算过程稍微作了些改变，决定利用一部分上次得到的结果, 省略掉前一部分计算。

因此，那天晚上，他辛辛苦苦地工作到深夜，直接将上一次计算後的部分数 一个一个打到输入卡片上，再送到计算機中。好，一切就绪了，开始计算！洛伦茨才放心的回家睡大觉去了。

第二天早上，洛伦茨兴致勃勃地来到MIT计算機房，期待他的新结果能验证上一次的计算。可是，这第二次计算的结果令洛伦茨大吃一驚∶他得到了一大堆和第一次结果完全不相同的数據！结果1和结果2千差萬别！

这是怎麽回事呢？洛伦茨只好再计算一次，结果仍然如此。又再回到第一種方法，计算後得到原来的结果1。洛伦茨翻来覆去地检查两種计算步骤，又算了好幾次，方法1总是给出结果1，方法2总是给出结果2。两種结果如此大大不同，必定是来自於两種方法的不同。但是，两種方法中，最後的计算程序是完全一样的，唯一的差别是初始数據∶第一種方法用的是计算機中存储的数據，而第二種方法用的是洛伦茨直接输入的数據。

这两组数據应该一模一样啊！洛伦茨经过若干次的检查和验证，盯着一个一个的数字反反覆覆看。啊，终於看到了。两组数據的確稍微有所不同，若干个数據中，有那厶幾个数字，被四捨五入後，有了一个微小的差别。

难道这厶微小的差别（比如，.000127）就能导致最後结果如此大的不同吗？洛伦茨百思而不解。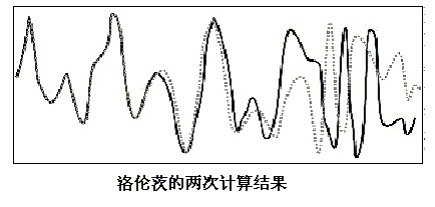

图（12.2）∶实线和虚线分别是洛仑兹的两次计算过程∶

初始值的微小差别，导致最後的结果完全不同。资料来自於(Ian Stewart, Does God Play Dice? The Mathematics of Chaos, pg. 141)

上面的示意图中，显示的是與洛伦茨氣象预报研究有关的结果。其中横坐标表示时间，纵坐标表示洛伦茨所模拟，也就是想要预报的氣候中的某个参数值，比如说，大氣氣流在空间某点的速度、方向，或者是温度、湿度、压力之类的变量等等。根據初始值以及描述物理规律的微分方程，洛伦茨对这些物理量的时间演化过程进行数字模拟，以达到预报的目的。但是，洛伦茨发现，初始值的微小变化，会随着时间增加而被指数放大，如果初始值稍稍变化，就使得结果大相径庭的话，这样的预报还有实际意义吗？

王二似乎恍然大悟∶“啊，难怪氣象台播的氣象预报经常都不准，招来骂声一片，看来他们也有他们的苦衷啊！”

张三说，图（12.2）这个曲线的意思比较容易理解，但是那个图（12.1）是怎厶得来的啊？我看它没完没了的绕圈圈，这與洛伦茨的氣象预报计算有什麽关系呢？

李四说，慢慢聽，当然有关系！当时的洛伦茨虽然甚感迷惑，却未必见得认识到了这个偶然发现的重要性, 也不一定能想到與此相关的‘混沌型’解将在非线性动力学中掀起一场轩然大波。尽管如此，洛伦茨毕竟是一位数学训练有素的科学家。实际上，洛伦茨年轻时在哈佛大学主修数学，只是因为後来爆发了第二次世界大战，他才服务於美国陆军航空队，当了一名天氣预报员。没想到经过战争中这幾年與氣象打交道的生涯，洛伦茨喜欢上了这个专业。战後，他便改变方向，到MIT专攻氣象预报理论，之後又成为了MIT的教授。他要利用他的数学头脑，还有当时刚刚初露锋芒的计算機和数字计算技术，来更準確地预测天氣，这是洛伦茨当时梦寐以求的理想。

可是，这两次计算结果千差萬别，这種结果对初始值的分外敏感性给了洛伦茨的美好理想当头一棒！使洛伦茨觉得自己在氣象预报工作中似乎显得山穷水尽、无能为力。为了走出困境，他继续深究下去。然而，越是深究下去，越是使洛伦茨不得不承认他的“準確预测天氣”的理想是实现不了的！因为当他研究他的微分方程组的解的稳定性时，发现一些非常奇怪和復杂的行为。

洛伦茨以他非凡的抽象能力, 将氣象预报模型里的上百个参数和方程, 简化到如下一个仅有三个变量及时间的、系数完全决定了的微分方程组。

dx/dt = 10(y - x)                               （12.1）

dy/dt = R*x ˉ y ˉ xz                          （12.2）

dz/dt = (8/3)z + xy                             （12.3）

这兒方程组中的x,y,z，並非任何运动粒子在三维空间的坐标，而是三个变量。这三个变量由氣象预报中的诸多物理量，如流速、温度、压力等等简化而来。方程（12.2）中的R在流體力学中叫做瑞利数，與流體的浮力及粘滞度等性质有关。瑞利数的大小对洛仑兹系统中混沌现象的产生至关重要，以後还要谈到。

这是一个不能用解析方法求解的非线性方程组。洛仑兹将瑞利数R=28，然後，利用计算機进行反覆迭代, 即首先从初始时刻x、y、z的一组数值x0、y0、z0，计算出下一个时刻它们的数值x1、y1、z1，再算出下一个时刻的x2、y2、z2┅┅如此不断地进行下去。将逐次得到的x、y、z瞬时值, 画在三维坐标空间中，这便描绘出了图（12.1）的奇妙而復杂的‘洛伦茨吸引子’图。