他自称是一个不关心政治的无神论者，他小时候玩发明，长大后玩数学，老了玩股票，什么好玩就玩什么，科学技术领域给玩了个遍。他不在乎这样东西有没有实用价值，不管那套理论有无学术意义，不考虑做的事情对公司有无贡献，不管这个问题是否重要，他只管好玩还是不好玩。

他的名字算不上广为人知，但他被誉为信息论之父。他，就是香农。

爱迪生的小亲戚

克劳德·香农 （Claude Shannon，1916年－2001年）出生成长于美国中部密歇根州一个小镇，有趣的是，香农的父亲给儿子取了一个和自己一模一样的名字[1]。老克劳德·香农是欧洲早期移民的后代，曾自主创业经商并取得成功，还做过当地的遗嘱检验法官。香农的母亲是德裔移民的女儿，当时少见的进过大学的女性，职业是语言学教师，还做过中学校长。香农还有一个姐姐，则得了一个和母亲一模一样的名字。香农一家在小镇上颇得人心：父母的职业和为人均受人尊敬。比香农大6岁的姐姐是个听话的孩子，优秀的学生，在学校各门功课成绩都很好，是现在被人们称为“学霸”式的人物。香农呢，他异常瘦弱，身上皮包骨头、脸庞棱角分明，言语不多，却又格外聪明，在小城镇里，他看起来永远像是那种刚刚被人欺负殴打过，令人心生同情的年轻小伙。

香农小时候最喜欢玩的是电气电子机械，他崇拜托马斯·爱迪生。不过后来他知道了，爱迪生竟然是自己的远房亲戚，便十分引以为傲。

使小香农自豪的，除了大发明家爱迪生之外，还有他的爷爷戴维·香农，爷爷是一位农场主兼发明家，颇具机械方面的才华，他对早期的洗衣机进行了一系列改进，拥有美国第407130号专利。

看来，发明的天赋也是能遗传的。小玩家香农有着一颗爱发明的心，将拨弄机械当作玩耍，他经常在家里捣鼓模型飞机、也制作用无线电控制的模型船。除了格外爱玩，他的童年却也分外孤独。因为当时他所处的小镇，人烟稀少，密歇根广袤的农地中，偶见几条街道和少许店铺，最近的朋友，也住在半英里之外。于是，香农发挥他摆弄物件的天赋，自建了一个可以与朋友联系的无线电台。香农的经验不断积累，高中毕业时，他已经是一名娴熟的发明家。他的发明包括简易升降机、后院小推车和通过带刺铁丝网传递加密消息的电报系统，等等。

图1：小时候的香农

除了发明小机械外，香农也表现出惊人的数学天赋。据说在8岁的时候，他就能做出他学数学的姐姐的高等数学作业。1934年，香农于17岁的时候，在《美国数学月刊》上发表了他的第一篇学术文章。他解出了一道数学难题，第一次向公众展示了他的数学才能。既会发明又能数学抽象，这两点成就了香农，使他造福于人类！

“最著名的硕士论文”

1932 年，16岁的香农进入密歇根大学，在他钟爱又好玩的数学和电子工程两个专业之间游荡，几年后，20岁的香农获得了这两个专业的本科学位。临近毕业时，公告栏上一则广告引起了他的兴趣。说的是时任麻省理工学院院长万内瓦尔·布什提供了一个研究生职位，合格者在读硕士的同时，还需要为布什教授操作管理他的一台微分分析机。据说这是一个重达百吨、由转动的轴承和齿轮构成的奇怪机器，在新闻中被誉为“机械大脑”或“思考机器” ：它能做高等数学，解出人类要花数月才能求解的方程！

那是第一次世界大战后，世界经济重心由欧洲转到美国，贝尔实验室、通用电气、麻省理工，成为美国电气工程应用的三大中心。随着机械和电气技术走向成熟，许多领域都对计算有迫切的需求。例如无处不在的微分方程，它们很少能有解析解，枯燥乏味的大量计算令人头疼。因此，布什教授设计了“微分分析机”来解决此类难题。用如今的术语来说，这部机器是模拟的而非数字的，其轮盘式积分器便是微分方程的物理模拟。无论如何，机器在当年还是很有用处，师生们蜂拥而来，排长队求用它以解决工程中的难题。布什已经难以应付，所以急需一名助手来操作、研究、和改进这个机器。

这个消息对临近毕业的香农来说，当然是天上掉馅饼，一个求之不得的好机会。而布什得到香农这样的机械电气都懂的全才也是正中下怀。于是，香农顺利进入麻省理工学院深造，那年头，MIT的校园里，便多了一道风景！香农“玩”名远播，有人说：这个校园里，如果你看见一个年轻人，目光深邃面庞瘦削，骑着一架怪异的独轮车，从你身旁飞驶而过，那多半是香农！

图2：香农和MIT的微分分析机（MIT Museum）

香农很快就深深地迷上了这架大玩具。那些旋转不止的模拟部件，分布在一个大大的平台式机器上，电源插上机器启动，整个房间喳喳作响。这种人们不喜欢的噪声，却令发明家欣喜无比。

微分分析仪是由布什和哈森于 1928 年到 1931 年建造的。两位工程师制造它是为了解决应用数学和物理领域中的实际问题，即求解微分方程。这实际上是一台由传动轴、齿轮和转盘组成的复杂的模拟计算机。在工程和物理学的动态系统中，如果两个物理量之间有某种数学关系，例如微分或积分的关系，便可以从这个动态系统的实际运作来完成该种数学计算，称之为模拟计算，该系统便是一台模拟计算机。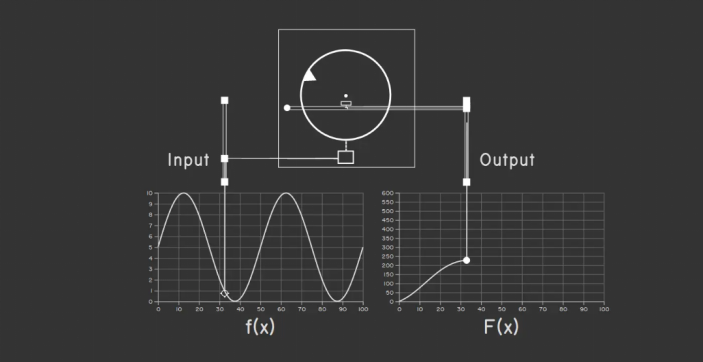

图3：模拟积分器

（https://sinclairtarget.com/differential-analyzer/）

布什的MIT微分分析仪最重要的构件是六个积分器，机械积分器的历史可以追溯到 19 世纪，它能够用动态系统中具积分函数关系的两个物理量，来模拟积分运算。机械积分器基本上是一个特别的求和机器，见图3。每一个积分器对应一个一阶微分方程。布什发现了一种将积分器串联起来解决高阶微分方程的方法。因此，他的包括六个积分器的微分分析仪，能够求解高达六阶的微分方程。

香农喜欢机械，当然对微分分析仪感兴趣，布什供给了许多元器件，希望香农能将机器朝更通用更自动化的方向改进，香农打算用上百个继电器来达到目的。他看着那些似乎不作声又偶尔咔嚓一下的继电器，觉得十分有趣。香农脑海中浮现出传递信息的摩尔斯码，继电器很像发送摩尔斯码使用的开关，香农又回忆起不久前上过的一门符号逻辑课程，其中有布尔代数。

布尔代数得名于自学成材的英国数学家布尔，他在1847年出版的一个小册子中介绍了这种代数逻辑系统，人们觉得这很有趣，但似乎没有什么实际用处。美国逻辑学家皮尔士曾经提出可以通过电气开关进行布尔计算，也没得到广泛的响应。

开关是电路器件，布尔逻辑是数学运算，两者看上去似乎风马牛不相及，但香农却感觉似曾相识，觉得这两者有相通之处，他想，这其中也许有文章可做！

接着，香农在1937年夏，到纽约的贝尔实验室实习了一个暑假，有关开关和布尔逻辑，这些令人困扰的想法，在他脑海里一直挥之不去。

香农进一步思考后发现，继电器“开、关”，或“是、否”，其实并不重要，关键的是这两种类型连在一起时，可以被逻辑中的“和”、 “或”、 “非”等等表述出来。例如，两开关串联即是“和”，并联则是“或”。其实，这就是在做计算。也就是说，电路可以进行逻辑运算！

布尔代数中的每个概念在电路中都有相对应的物理表示。操作电路继电器的人在实际上知道这些电路原则，但他们没有把他们所做的事情抽象成布尔代数的数学模型。因此，布尔逻辑可以实现到符号再到电路的飞跃。只要定义好了逻辑符号，由继电器组成的复杂电路的效应，便可以表示成多个变量二进制的代数方程式。比如，以下方程式：

x'y'z + x'yz + xy'z + xyz' + xyz

可以表示一个3个继电器构成的电路。

这个21岁的青年，觉得这个想法非常有趣，他兴奋激动于自己从开关盒子和继电器中看到了别人没有看到的东西。1937年秋，香农在美国华盛顿哥伦比亚特区向评委会演示了自己的硕士论文《继电器和开关电路的符号分析》，并在第二年发表在期刊上。

香农在论文中，分析了电话交换电路和布尔代数之间的类似性，用布尔代数分析并优化了开关电路。香农的这篇硕士论文，具有划时代的意义。它奠定了数字电路的理论基础。因此，有科学家评价这篇论文是“有史以来最重要的一篇硕士论文”，“从艺术到科学上改变了电路的设计” 。香农将电路设计的技术变成了一门科学！

因为这篇论文，香农获得了电子工程界的大奖——美国Alfred Noble协会的美国工程师奖。这给香农带来了在电子工业界大展拳脚的好机会，然而，他却似乎从这个领域消失了。

香农于1939年夏天，来到了冷泉港，抵达了美国最顶尖的基因实验室。原来他改弦更张，从电子工程跨界到了生物，试图将他的“代数”理论应用于新兴的遗传学，他玩起基因来了！两年后，他完成了博士论文——《理论遗传学的代数》，用线性代数描述不同遗传性状在遗传中的可能性，用一种奇怪的符号代数，来预测性状是如何代代相传的。

图4：香农的博士论文丨图源：dspace.mit.edu

那时候，尚未发现DNA螺旋结构，也不知道遗传密码等等，香农是完全在自己头脑中构想遗传机制的，并企图用代数理论模型去描述遗传现象。

1940年香农以此论文，获得了麻省理工的数学博士学位，并且得到了普林斯顿高等研究院的博士后机会。在那儿，香农能自由地跨学科工作，他有机会与外尔和冯·诺依曼等数学家讨论他的想法，还偶尔遇到爱因斯坦和哥德尔[2]。

计算、密码、信息

被誉为计算机之父，比香农大4岁的图灵，比香农更为公众所知。但实际上，他们两人的思想和经历有很多相似之处：都对机器计算感兴趣，都研究过密码，都曾经将数学应用于生物学，都喜欢思考人工智能的问题，等等。遗憾的是，他们一个在英国一个在美国，生前很少见面。感慨的是他们后来的境遇：图灵因性取向受迫害早逝，香农“玩”到八十多岁高龄，老年痴呆去世。

二战期间的1943年初，在美国贝尔实验室的餐厅里，两位天才少年一见如故。图灵那年被派往美国，来到新泽西，目的是为了给大西洋两岸传输的通话内容加密，使敌人无法监听盟军情报。香农战时从普林斯顿高等研究院，转到了贝尔实验室，研究如何对华盛顿到伦敦的通信线路进行加密的课题。尽管我们现在知道他们那时都在研究密码，但各自的专题项目，分别是两个国家的绝对机密，所以两人都不知道对方在搞啥？饭堂里的闲聊也不涉及解密技术。不过，他们有太多的共同话题和想法，那些日子他们闲聊的是“会思考的机器”，也就是理想的计算机的极限是什么的问题。那年代还没有人知道计算机到底将是什么模样！所以他们的探讨大多基于数学和逻辑，两人想都没想过，他们将在科学史上各自开辟一个独立的领域。 

图灵从更为数学的视角出发，认为理想的计算机应该是纯粹逻辑演绎的设备，而热衷于发明的香农则考虑得更广泛，他认为计算机将是一种社会性的工具，甚至能处理音乐等非逻辑性的东西。

于是，图灵向香农展示了他 1936 年的论文，就是定义了现在所谓的“通用图灵机”的那篇文章。这给香农留下了深刻的印象，因为其中的许多想法与他自己的想法不谋而合相辅相成。图灵的工作使香农灵感忽现，他发现，有些看似截然不同的事物其实具有共同的本质。

图灵在与香农交流“通用图灵机”的过程中也大为振奋，两人讨论时说话的声音不由自主地越来越大，甚至引起周围用餐人纷纷注目。香农从电子工程师的视角，看到了图灵机的实用价值，这点使图灵激动不已，也让图灵站到数学之外，对图灵机的意义重新思考。会思考的机器，或许真的可以用电路而变成现实吗？图灵觉得这太有趣了！因此，他在离开美国之前，买了一本电路入门书，把它带到回英国的船上，如饥似渴地阅读起来。

图灵在密码方面的工作主要是破解了德国人发明的ENIGMA密码，这种密码被德军广泛使用，包括定位出没于大西洋运输线上的潜艇。当年的英国人和法国人都认为ENIGMA是不可破译的，图灵率领着大约200多名精干人员进行密码分析，他们掌握了破译该密码的一整套方法，从而了解了德军的动向，掌握了战争的主动权，为英美联军击败德国做出了突出贡献。

香农在密码学方面的工作，则与其后来关于通信理论的关系密切。香农自己说，他对通信理论和密码学的战时见解是同时发展的，“它们是如此紧密地结合在一起，你无法将它们分开”。

实际上，香农更早就有了模糊的想法。在1939年初，他在写给布什的信中说到，除了微分分析机外，他还在考虑一个自认为更重要的问题：“我一直在研究传递信息的一般系统的某些基本属性，它们包括电话、广播、电视和电报等。几乎所有的通信系统都可以归结为如下的一般形式：信息从发送方到接收方，其中涉及三个“时间函数”，待传输的初始信息fi(t)，中间信号f(t)，以及最终输出ff(t)。”，这就是香农设想的通讯过程，见图5a。 

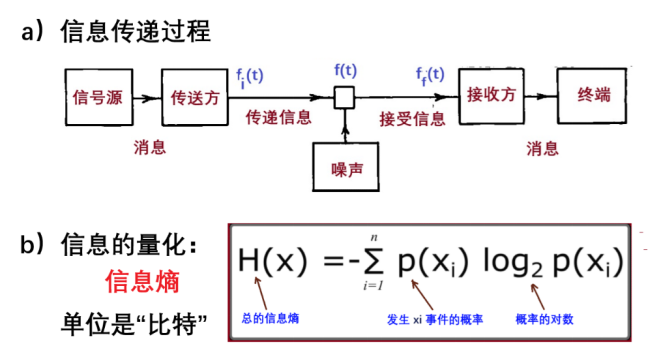
图5：信息论

香农认识到，真实的系统中还存在噪声，并且他试图证明一些定理，来数学地描述通信系统。在贝尔实验室，研究数字通信中的信息保密和隐藏技术的一系列工作，成就香农建立了现代信息论。1948年，作为此项工作的总结报告，香农发表了论文“通信的数学原理”[3]，1949年，他又发表了“噪声下的通信”一文。几篇文章阐述了信息论的基本内容。

我认为信息论是科学中最美的理论之一，它美在哪里呢？美在其通用性，美在它的简洁，并且，尤为可贵的是：它美在简洁与深奥并存[4]。

图5中简单的两个图，就几乎概括了信息论的全部内容。其中的图a描述了信息的传输过程，这不仅适宜于通讯，还有计算机、遗传学、生物学、物理及化学过程等。事实上，信息及其传输过程无处不在，因此，信息论几乎可以推广应用到所有领域。

如何用数学语言描述信息传输过程？为此香农定义了信息的基本概念，见图5b。

什么是信息？信息的概念既抽象又多变，信息既不是物质，也不是能量，要给信息这个人人明白又抓不住摸不着的东西，下确切定义是不容易的。可以毫不夸张地说：幸亏有了香农！作为玩遍种种技术的工程师，香农深刻理解“信息”之本质；作为善于抽象的数学家，香农明白必须首先给信息一个定量描述，量化后才有理论！物质和能量都是可度量的，如何度量信息呢？

香农借用了热力学中的一个词：熵。或许在学术界关于信息理论的辩论中，冯·诺尔曼和维纳（ Wiener）对香农都有所启发，但无论如何，是香农最终提出了“信息熵”的概念和表达式（图5b）。信息熵公式中，香农天才而巧妙地将信息与概率联系起来，揭示了信息是“不确定性的度量”这个微观本质。

用过计算机的人对“比特”这个词不会陌生，但你可能不知道，比特是香农定义的信息的单位，计算过程就是传递信息，所以自然而然地，比特也成为了衡量计算机运算及储存能力的重要指标。

这儿举“语言信息”为例，简单理解一下图5b的公式。例如，人们说一句话，其中的信息是一个“字符串”，例如“我是马斯克”，这是5个汉字符号组成的字符串。信息熵H是由字符串中所有符号xi的概率p(xi)乘以概率的对数再求和所确定的，每个符号xi的信息量，与符号通常出现的概率（不确定性）有关。因此，香农的信息论公式，在信息与不确定性和混乱程度之间架起了桥梁，这是信息与自然界的深层联系。

传奇人物销声敛迹

这两年最火的科学新闻首推“AI”，即人工智能，殊不知香农也是AI先驱之一。

香农在 1950 年左右发表的一篇论文《计算机下棋程序》里描述了如何让计算机下国际象棋。此文被认为是最早发表的关于计算机下棋和使用计算机解决游戏主题的文章之一，其中他提出了限制国际象棋游戏中要考虑的可能性数量的基本策略。香农给出了国际象棋的复杂度，大约是 10¹²⁰ 量级（被称为“香农数”），不过他在论文中给出了一个更为明智的算法，可以大幅度地简化计算。1997 年，由这篇论文演化出来的算法，在“深蓝”中运行，成功击败了卡斯帕罗夫。

香农大多数学术成果都是上世纪60年代之前完成的，然后，他就不“玩”学术而玩别的去了。

图6：爱“玩”的香农（图片来自网络）

“你无忧无虑的秘诀是什么？”一位采访者在香农临终前询问他，香农回答说：“我一生顺其自然，实用性不是我的主要目标……”。总结香农能无忧无虑地“玩”，首先肯定是抛弃了世俗名利的纷扰，好奇心驱动他对大自然的探索。终其一生，香农都在玩游戏、发明游戏、摆弄小机械和小装置，即便成年之后也保持着那份童真之心。

1951年，香农发表论文“介绍一个走迷宫的机器”，写的是他制造的名为“忒修斯”（Theseus）的机器老鼠，迷宫配置灵活，可重新布置任意修改。机械鼠在 25 个方格迷宫中移动，通过反复试探后自己找到迷宫的出路。老鼠第一次穿过迷宫后，如果将它放置在之前去过的地方，它可以根据之前的经验，直接就到达目标。如果被放置在不熟悉的区域的话，便会被编程为“搜索”，然后逐步搜索直到成功。成功后，它会将新知识添加到其记忆中并学习新的行为，你看看，这像不像如今的AI学习机器？

香农是一个狂热的独轮车爱好者，他喜欢设计和制造各种稀奇古怪的独轮车。他发明了名为 THROBAC 的罗马数字计算机和杂耍机；他建造了一个可以解决魔方难题的设备；他还与索普共同发明了第一台可穿戴计算机，用于提高玩轮盘赌时的赔率。他设计了一个“心灵阅读”机器，通过观察和分析弈棋对手过去所做各种选择的样本，能够相当准确地猜测到对手下一步棋的走法。

虽然香农一直是MIT教授，但因为痴迷玩发明创造，后来他不发论文也不出席专业会议，便逐渐淡出了公众的视线。非常戏剧性的一刻发生在1985年的英国国际信息理论研讨会上：香农出人意料地现身会场，很多与会者甚至不知道他仍然在世。这位谦虚羞涩的名人被人认出来后，被粉丝们团团围住。最后，还只好不情愿地在晚宴上登台，被主持人隆重地介绍为“我们这个时代最伟大的科学巨匠之一”。掌声平息后，香农冒出一句：“这真是太可笑了！”然后，他把手伸到衣服口袋里，变戏法一样掏出了3个球，竟然当场玩起了杂耍。

会玩杂耍的人千千万，世界上的发明家也不计其数。然而，会玩又能从中悟出大自然奥妙的人，唯香农也。谁能玩密码联想到信息论？又有谁玩象棋时思考AI？谁能玩了抛球杂技便提出一个“抛球定理”？哪一个独轮车骑手，非要将独轮车的运动转化为方程式呢？别无他人，唯香农也。

到了1980年代，香农的记忆力开始严重衰退，后来患上了老年痴呆症。这位独特而有趣的天才，在与疾病抗争了很长一段时间后，于2001年2月24日辞世，享年84岁。

参考文献：

[1]香农传，作者：[美]吉米·索尼，[美]罗伯·古德曼译者：杨晔出版社：中信出版集团出版时间：2019-02

[2]信息简史，作者：[美]詹姆斯·格雷克译者：高博出版社：人民邮电出版社出版时间：2013-12

[3]Shannon C E. A mathematical theory of communication[J]. ACM SIGMOBILE Mobile

Computing and Communications Review, 2001, 5(1): 3-55.

[4]科学网—“熵”- 信息世界也逞强- 张天蓉的博文：

https://blog.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&quickforward=1&id=987651

（本文于2/3/2024首次发布于微信公众号“知识分子”）