第十八章﹕生态繁衍和混沌 “生命的诞生和消亡,生儿育女,生老病死,是人人都关心的问题。你们没想到吧,这也和混沌沾上了边……” 在一个小教室里,王二嘻皮笑脸地开始了他对生物繁衍中的混沌现象的介绍。一年多过去了,三个朋友的‘分形和混沌’讨论会已经扩展到了十几个人,多数是大学生,也有几个研究生,比如李四和张三。 中国人对马尔萨斯的名字并不陌生,对他的“人口论”更有切身的体会。托马斯·马尔萨斯1766年出生于一个富有的英国家庭,父亲丹尼尔是位哲学家,与著名法国哲学家卢梭是好朋友。没想到丹尼尔这个乐观的学者却生出了托马斯这个对世界前景充满悲观论调的人口学家。1798年,托马斯·马尔萨斯发表他著名的《人口学原理》,对人类作出一个悲观的预言:人口将以几何级数增长,超越食物的算术级数增长,因而,最后将必然导致战争、瘟疫、饥荒等等人类的各种灾难。 马尔萨斯的人口论基于一个很简单的公式: Xn+1 =(1+r)Xn = kXn (18.1) 公式中的Xn+1代表第(n+1)代的人口数,Xn代表第(n)代的人口数,r = (Xn+1- Xn)/ Xn,是人口增长率。k=1+r通常是一个大于1的数,因而,人口数便以k的幂级数增长。我们假设迭代次数以‘年’计算,有了这个公式,从某年一个初始的人口数出发,便可以推算出下一年、再下一年、再再下一年的人口数来。 这儿,马尔萨斯犯了一个错误,他把各种灾难作为人口增长之后的结果来处理。而实际上,战争、瘟疫和饥荒是伴随着人口繁衍而同时发生的,必须在方程中就将这些因素考虑进去。因此,后来的学者们对这个理论进行了修正,在公式(18.1)的右方加上了一个负的平方修正项,变为: Xn+1 = kXn – (k/N)·(Xn)2 (18.2) 这个非线性修正项则是反映了诸如食物来源、疾病、战争等等生存环境因素对人口的影响,负号表明这种制约导致下一代人口Xn+1的减少。这就是生态学中著名的逻辑斯蒂方程,它不仅仅可用于‘人口’的研究,也可用于对其它生物繁衍,种群数量,诸如‘马口’,‘鸟口’,‘虫口’等等的研究。上面的(18.2)也可改写成: xn+1 = kxn – k·(xn)2 = kxn·(1-xn) (18.3) 公式(18.3)中,我们将大写的X变换成了小写x,用以表示相对人口数:x=X/N,N是最大人口数。 从(18.3)明显地看出,下一代的xn+1,是上一代的xn和(1-xn)的乘积。当xn增大时,(1-xn)则减小,因而逻辑斯蒂方程同时考虑了鼓励和抑制两种因素。此外,由于(18.2)中的第二项是个非线性项,听到‘非线性’这个词,你们就要小心啊!非线性的效应使得方程中暗藏了‘混沌’这个魔鬼。 “不过没关系,魔高一尺,道高一丈。曾记否?我们有计算机,那是能让混沌魔鬼现出原形的照妖镜……”王二对递给他矿泉水的林零笑了笑,插了句玩笑话后,继续他的演讲。 计算机技术寻找‘混沌’魔鬼,的确功不可没。20世纪70年代,继洛伦茨之后,各个领域的人们都开始注意用计算机研究混沌现象,寻找各种非线性方程的奇异吸引子。那时,英国有个罗伯特·梅,来到美国普林斯顿大学,他看上了生态学中这个既简单而又非线性的逻辑斯蒂方程。 
图(18.1):澳大利亚出生的英国生态学家罗伯特·梅 罗伯特·梅1938年生于澳大利亚悉尼,是个在各个领域涉猎甚广的科学家。他最开始学的是化学工程,后来转向理论物理。作为一个理论物理博士和教授工作多年之后,罗伯特·梅对理论生态学、人口动态研究、生物系统的复杂性及稳定性等问题发生了浓厚的兴趣。因此,他在普林斯顿大学任教期间(1973-1988),研究方向便完全转向了生物学。 罗伯特·梅将逻辑斯蒂方程用来研究昆虫群体的繁殖规律。不过,他并不是简单地跟随气象学家洛伦茨的脚步,画出逻辑斯蒂方程的奇异吸引子而已。他的研究有他的独到之处,他感兴趣的是方程(18.2-3)中的参数k。罗伯特·梅发现,参数k的数值大小,决定了混沌魔鬼出现或者不出现!当k值比较小的时候,混沌魔鬼消声敛迹无踪影,只有当k大到一定的数值时,混沌魔鬼才现身。 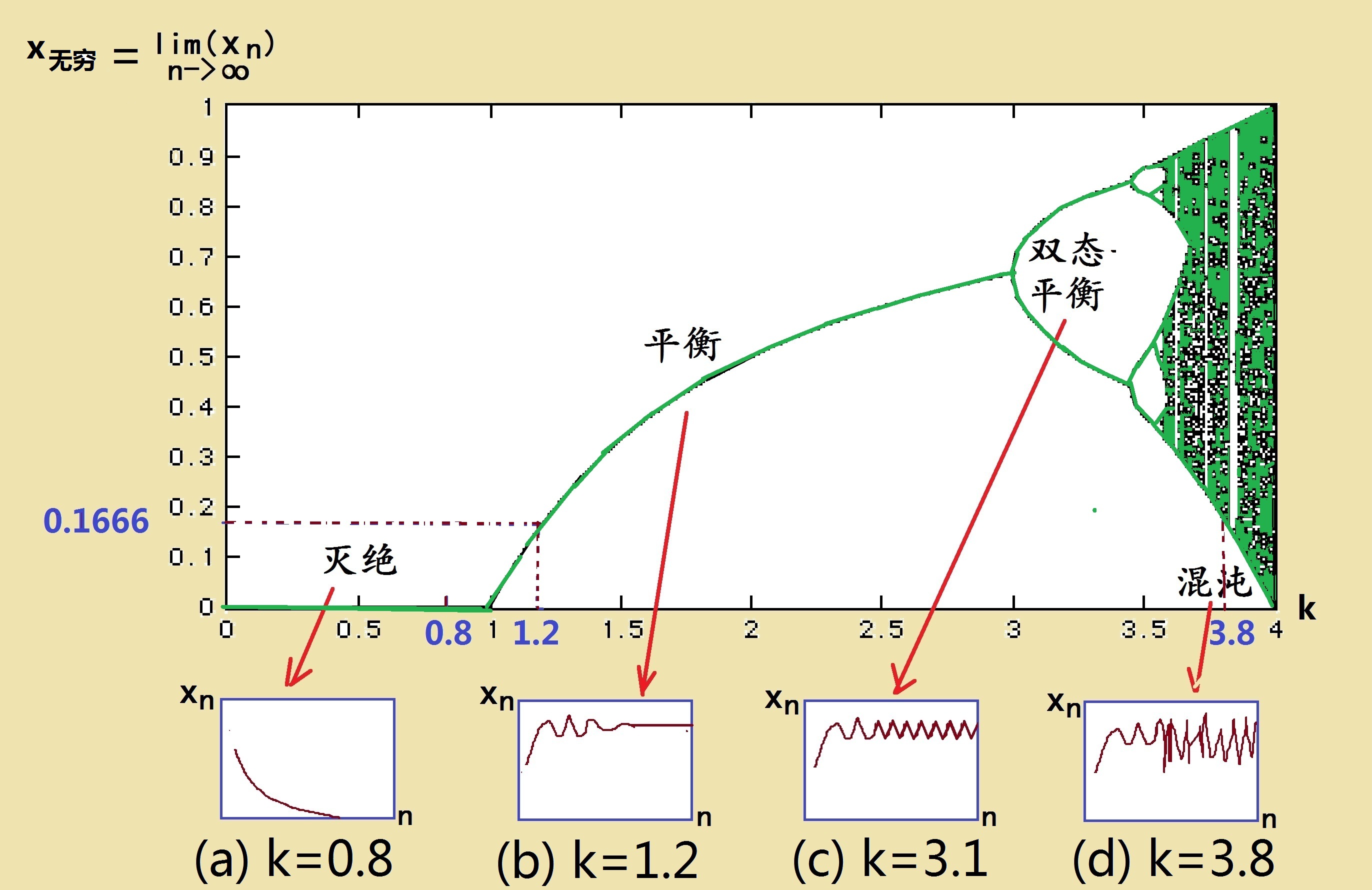
图(18.2):对应于不同的k值,逻辑斯蒂方程解的不同长期行为 罗伯特·梅于1976年,在英国《自然》杂志上发表了他的研究成果—《表现非常复杂的动力学的简单数学模型》[1] ,论文引起学术界的极大关注,因为它揭示出了逻辑斯蒂方程深处蕴藏的丰富内涵,这已经远远超越了生态学的领域。 现在,让我们更直观地解释一下方程(18.3)和图(18.2)的意义,看看方程(18.3)是否具有混沌魔鬼的行为?请注意,这儿所说‘行为’的意思是指‘长期行为’。也就是说,我们需要研究的是:用方程(18.3)作迭代,当迭代次数趋于无穷时,群体数的最后归宿,是经典的还是混沌的?图(18.2)中的绿色曲线,是罗伯特·梅的研究结果。他用绿色曲线画出了最后的相对群体数x无穷随着k的增大而变化的情形。x无穷是当n趋于无穷时xn的极限。图(18.2)中下面四个小图,则是在一定的k值下作迭代的过程。必须注意,在方程(18.3)及图中的xi是‘相对’群体数,可以把它规定为是相对于一个最大的群体数N而言,比如,我们可以取N = 10000,群体数的初值取为1000,也就是说,某种生物最开始时有1000个,那么,不难算出相对群体数的初值,x0=1000/10000=0.1。 这个看上去有点奇怪的绿色曲线可以按照k的大小,曲线的不同形态分成好几段,图中分别记为:灭绝->平衡->双态平衡->混沌。 因此,罗伯特·梅发现,对逻辑斯蒂方程的混沌魔鬼来说,参数k的数值太重要了。增大k的数值可以让混沌魔鬼诞生出来!但是,混沌魔鬼是怎样生成的?为何k变大就能形成魔鬼呢?于是,罗伯特·梅便详细地研究了混沌魔鬼诞生的过程,对此我们将在下一章继续讨论。 参考资料: 【1】May, R. M. "Simple Mathematical Models with Very Complicated Dynamics." Nature 261, 459-467, 1976. http://matematicas.euita.upm.es/GRuiz/ICF/Pdf/May76.pdf 上一篇∶混沌遊戲 返回目录 下一篇∶从有序到混沌 |
