| 无论是量子信息、量子密码、量子计算等等,所有想要在计算或通讯中应用量子力学规律的领域,都离不开一个基本的位元∶量子比特。从前面的章节我们已经了解到,量子比特是一个量子态,由于量子态的叠加性质,n个量子比特能够表示的状态数比n个经典比特能表示的状态数多得多,因此,量子比特比经典比特听起来更强大、更有用多了。不过,我们也知道,量子态是不确定的、难以对付的。除此之外,它还有个经典比特完全没有的性质∶不可克隆定理。 量子态不可克隆定理说:一个未知的量子态是不可克隆的。有学者在1982年(见参考资料)从量子态叠加原理的推论,而证明了这个定理。在此,我们只是从测不准原理来粗浅地理解这个定理∶从经典‘克隆’的意义上说,要想精确地复制一个物品,首先就要得到(测量)这个物品的所有的信息。然而,对一个遵循量子规律的系统(比如量子比特),我们不可能同时精确测量它的所有物理量,因为根据“海森堡测不准原理”,在同一时刻以相同精度测定量子的位置与动量是不可能的,我们只能精确测定两者之一。 从量子论的观点而言,测不准原理应该被称为“不确定性原理”更恰当一些。但如果使用经典的图像来想象微观世界的话,叫做“测不准”可能还更容易理解。比如,以测量电子为例,所谓测量,一定要使用测量方法和工具,要对电子进行测量,最好的方法就是使用激光去与电子相互作用。原子中的一个电子,从经典角度看,它的运动轨道是如此之小(10-10米),它的运动速度又是如此之快(106米/秒),在这种快速运动情形下的电子,被测量它的光子顶头一撞,速度和位置都全变了,又怎厶可能测得准呢? 比如说,利用光被电子散射,可以测量电子的位置,但不可能将粒子的位置确定到比光的波长更小。所以,要想将位置测量准确,必须用更短的波长的光,而波长更短的光子具有更大的能量,就对电子的速度产生更大的扰动,使得速度更不能测准,反过来说也是一样。 “量子不可克隆定理”,是指在不知道量子状态的情况下复制单个量子是不可能的,因为要复制单个量子就只能先作测量,而测量必然改变量子的状态。我们在介绍量子比特时提到过,一个qubit有两个自由度,由于测不准原理的限制,我们无法准确地测量这两个自由度,因此也就无法精确地克隆出这个量子比特的状态。 量子态不可克隆,这是在通讯中使用量子比特的极大优越性。这个优点保证了量子密码、量子通讯的安全性。但是,也由此而为它在通讯上的真正应用设置了难以逾越的障碍。在我们现代社会中铺天盖地的通讯网中,每秒钟都在复制、传输着天文数字个比特的信息。仅拿一台ADSL上网的计算机来说吧,如果网速是512Kbps,那就是每秒钟传输51.2丌个比特。可是,量子比特怎厶办呢?连复制都不行,如何传输呢? 科学家总能想出一些窍门,不能克隆没关系,我们照样传输它们!这就是近年来在这个行业内热门的话题,叫做“量子隐形传输”。 美国的国际商业机器公司(IBM)不愧是计算机行业的龙头老大,它不仅引领着传统的经典计算机的研发和制造,在量子计算机的研究方面,几十年来也独树一帜,不论在理论方面,还是实验方面,都进行了大量的研究工作。比如上一节中提到过的“可逆计算” 的IBM科学家R. Landauer,他在1961年对“可逆计算”的研究就与量子计算机研究有关。 “量子隐形传输”的理论设想,是由另一位IBM研究中心的研究员,查尔斯·亨利·贝内特最先提出来的。贝内特1943年生于美国纽约市,既是一位物理学家,又是信息理论学家,是现代量子信息理论的开山鼻祖之一。 
贝内特等提出“量子隐形传输”的六人团队 照片来自网络∶http://researcher.ibm.com/view_project.php?id=2862 贝内特1970年从哈佛大学得到博士学位後,于1972年加入IBM的研究队伍。在IBM,他做了大量有关量子信息学方面的工作。他曾经提出对麦克斯韦妖的重新解释,他与同行们合作开发了BB84量子密码协议,并建立了世界上第一个量子密码的工作演示。 1993年,Bennett等六人团队,在“物理评论快讯”上发表文章,提出“量子态隐形传输”的设想。设想将一个未知量子态的完整信息,合作通过两个独立的通道(经典和量子)发送出去,在新的远 的位置重新组合後,产生一个在发送过程中被破坏了的原始量子态的精确副本。 贝内特等人的想法可由下图说明∶ 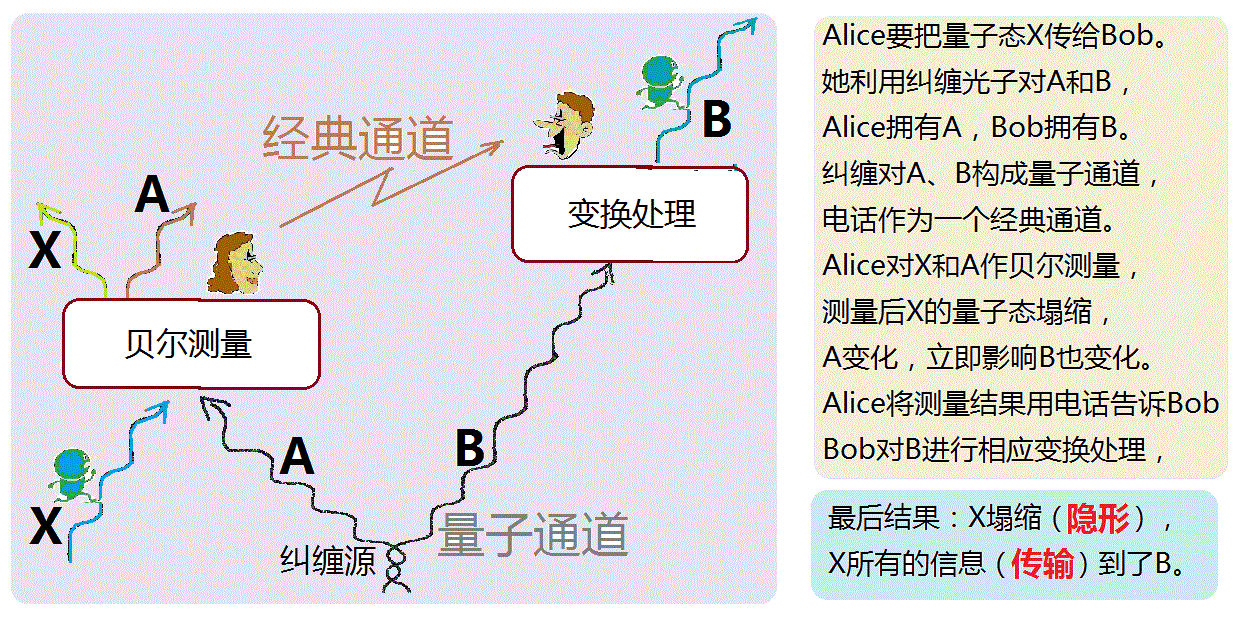
图中左边的Alice,想要把量子态X传给Bob。她利用纠缠光子对A和B,Alice拥有纠缠光子中的A,而Bob拥有B。纠缠光子A、B构成量子通道,电话或是互联网可作为经典通道。首先,Alice对需要传送的X和她手中的A作“贝尔测量”。测量後,X的量子态塌缩了,A也发生变化。因为A和B互相纠缠,A的变化立即影响B也发生变化。然而,Bob无法察觉B的变化,直到从经典通道得到Alice传来的信息。比如说,Alice在电话中将测量结果告诉Bob。然後,Bob对B进行相应的变换处理。最後,B成为和原来的X一模一样。这个传输过程完成之後,X塌缩隐形了,X所有的信息都传输到了B上,因而称之为“隐形传输”。 读者从上面的说法中,可能会提出以下几个问题∶ 1。既然是仍然要使用经典的通道,那为何还要量子通道呢?用经典通道把全部信息都传过去好了。 2。在Alice这边的方框中,“贝尔测量”是什厶意思? 3。在Bob那边的方框中,“变换处理”是什厶意思? 提出第一个问题的人,一定是因为不记得“量子不可克隆定理”了!根据这个原理,我们是不可能得到量子态X的全部信息的,所以,从经典通道就不可能传递所有信息。实际上,我们可以用经典电传(FAX)的例子作比喻,就知道,要想得到经典物体的“所有信息”,是很困难的。 用电传机发送电传的过程,可以用上面量子隐形传输示意图简化,而得到如下图所示的“电传示意图”∶ 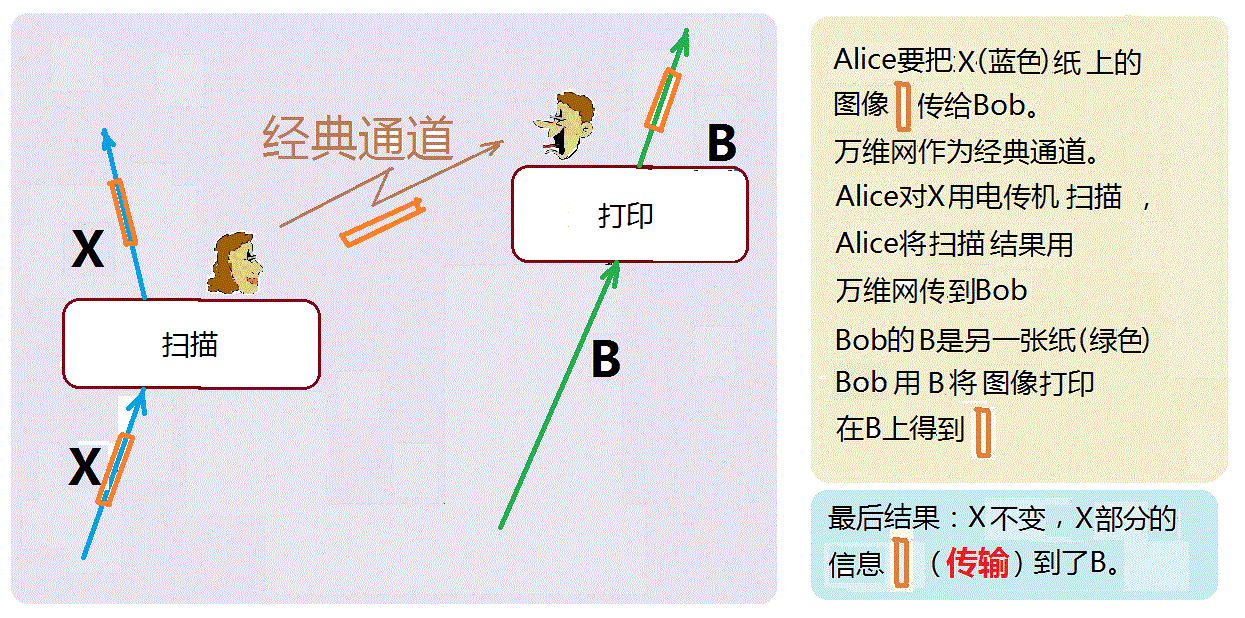
从上图看到,比之“量子隐形传输”,电传过程少了一个纠缠对腹成的量子通道。在电传过程中,首先,Alice将上面印有图像信息的蓝色纸X进行扫描,得到需要传输的图像信息。然後,将此信息从经典通道(互联网)传给Bob。Bob收到图像後,用另外一张纸B(绿色)将图像打印出来。在这种传递过程中,“图像”只是X的一部分信息,X的其他信息,诸如纸张材料、颜色、大小、厚度等等,并不能从扫描过程得到,也没有被传递过去。况且,即使是Bob知道了这些性质,造出一张表面看起来完全一样的纸来打印图像,後来的B也不能说是和原来的X一模一样的。因为肯定不可能保证每个分子都一样吧。 而在量子隐形传输中,最後的B是和原来的X完全一样的。换言之,电传时传输後所复制出来的,只是纸上图像的信息,没有复制出任何‘实体’本身。量子隐形传输却有点像是∶从得到实体的完整信息,而复制出了‘实体’本身,尽管只是一个小小的量子态!这样说,人们可能要心情激动、欢呼雀跃∶“啊!科幻电影中远距 传物的时代就要来临了!” 其实远远不是这样,那种想法是一个误解。我们这儿谈论的“复制”不过只是一个量子现象,完全不知道如何才能复制一个较大的、真正的物体。即使是与海边一颗小小的沙粒的传输复制,也还相距十万八千里。 上面提到的与量子通道有关的“贝尔测量”以及“变换处理”,留到下节讲解。 参考资料∶ 量子不可克隆定理∶Wotte rs W . K . and Zurek W . H ., Nature . 299 (1982 ) , 802 量子隐形传输∶C.H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, and W. Wootters, "Teleporting an Unknown Quantum State via Dual Classical and EPR Channels", Phys. Rev. Lett. vol. 70, pp 1895-1899 (1993) 上一篇∶量子计算机 下一篇∶量子传输(二) |
