後来，阿斯派克特在提到他80年代所做的那三个实验时说∶“令我感到自豪的，除了实验本身之外，是我们的工作引起了人们对贝尔定理的广泛关注。”事实的确如此，自阿斯派克特的实验之後，更多物理学家们开始思考量子力学的基本原理，因为现在，‘非定域特征’已经不仅仅是像过去的爱因斯坦和波尔之间所进行的那种没完没了的哲学之争，它成为一个在实验室里可以检验的热门课题。人们从各个方面，用不同的方法，来验证量子纠缠态存在的事实，从而也检验量子力学的非定域特征。

产生纠缠态的纠缠光源，也与时俱进，从技术和原理方面都大大得到改进。美国罗彻斯特大学的伦纳德·曼德尔（Leonard Mandel），利用激光照射在非线性晶体上产生的自发参量转换，来产生更为稳定可靠的纠缠光子对。曼德尔的学生杰夫·金伯尔（H. Jeff Kimble）後来在奥斯丁德州大学和加州理工学院，改进了量子纠缠光源，并完成了一系列量子光学有关的突破性实验。中国著名的光学专家，山西大学光电研究所彭堃墀院士，曾在美国加州理工学院金伯尔的实验室里工作过。当时，彭堃墀院士通过自发参量下转换的方法，产生了稳定的连续变量纠缠源，并首次用实验证实了连续变量的EPR佯谬。

另一位华裔物理学家，美国马里兰大学的史砚华（Yanhua Shih）也做了一系列有趣的实验，包括著名的‘量子擦除实验’，以及我们在第五节中提到过的，约翰·惠勒提出的延迟选择实验。史砚华的实验结果非常精确地符合量子力学的理论预测。在史砚华的一系列实验中，最有趣的也与此文最有关系的，是一个被称为“幽灵成像”的实验。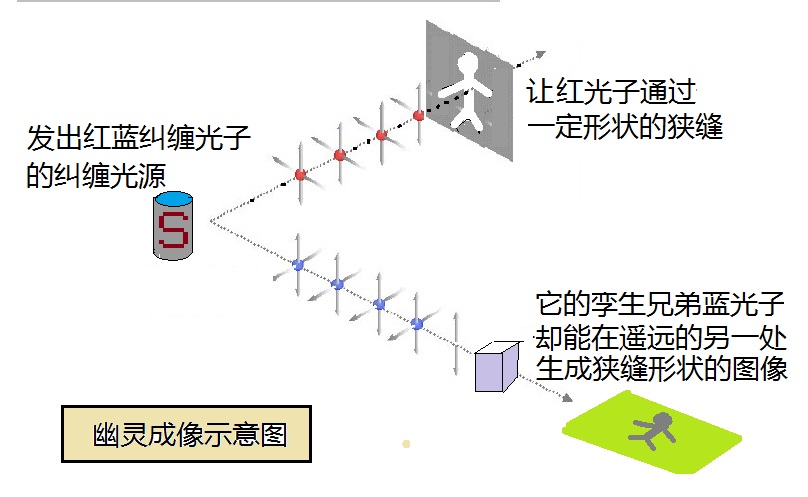

图一∶幽灵成像原理

如图一所示，纠缠光源发出互为纠缠的红光子和蓝光子。经过偏振器之後，红蓝光子分开向不同的方向传播。在史砚华等人的实验中，与通过了狭缝的红光子互相纠缠的蓝光子被识别分离出来，投射到一个屏幕上。人们发现，红光子道路上经过的狭缝图像，像幽灵鬼影一般，呈现在蓝光子投射的屏幕上。

下面的图二是史砚华等人的实验设计及结果图。在他们的实验中，狭缝形状不是一个鬼影，而是四个字母“UMBC”（图二右上角），这是马里兰大学的英文缩写。图二右下角的实验结果显示，那些经过了狭缝的光子的孪生兄弟们，在实验室的另一端遥相呼应，幽灵般地呈现出了与狭缝形状一致的图像∶UMBC。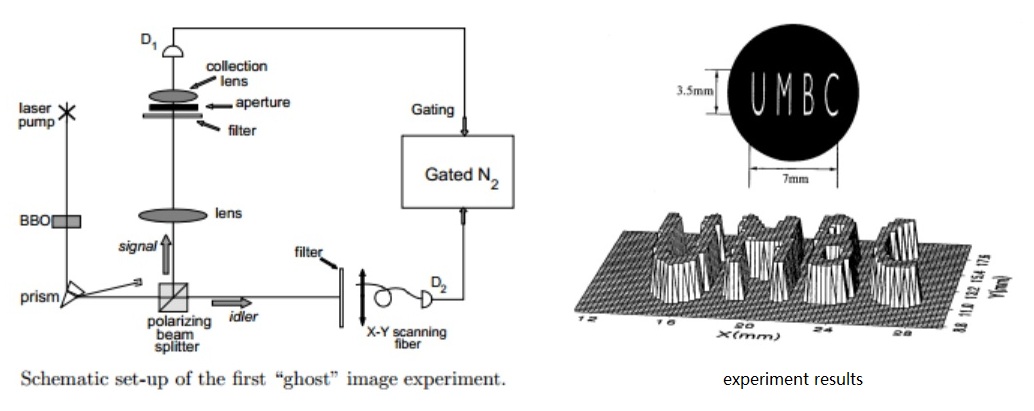

图二∶扫描自史砚华等人的文章

以上‘幽灵成像’这个生动的实验，给了我们一些什厶启示呢？首先，我们再一次直观地认识到∶光量子的纠缠现象是确确实实存在的，否则，红光经过的狭缝，怎厶会由完全分道扬镳的另一路蓝光在远处成像呢？如果不使用‘量子纠缠’这个概念，用经典光学的理论，是解释不了这个现象的。因此，这个实验利用了纠缠光子对，这是第一关键处。但是，仅此还不足够，因为红蓝光子是在很早就分开了的，只有一部分红光子穿过了狭缝，却是所有的蓝光子都到达了这边的屏幕。这‘所有的’蓝光子成不了任何图像，必须把穿过狭缝那些红光子的蓝色孪生兄弟一个一个找出来，只有让它们排队站在屏幕上，我们才能看到图像。如何寻找这些孪生蓝光子呢？类似于可以从比较一对兄弟的DNA来判断他们是不是同卵的双胞胎一样，实验物理学家们也自有他们的办法来鉴定红蓝孪生光子。不外乎是测量它们的关联函数之类的，我们在此不详细叙述。

或者，我们可以从上面一段话总结出一些要点。要完成幽灵成像，必须有两个通道∶量子通道和经典通道。量子通道提供了与所有红光纠缠的蓝色光子，经典通道提供分离出特别的孪生子的方法。对成像来说，这两个通道缺一不可。这里，我们要再次强调一下这个“量子经典”两通道的说法，是因为以後我们在谈到‘量子隐形传输’时还会用到它。

幽灵成像的实验生动有趣，对两个量子纠缠的深奥概念给了一个直观的演示。但是，由量子纠缠而引发的量子通讯方面应用研究的新篇章，却是从GHZ三个人对三粒子纠缠态的研究开始揭开的。

上一节中，我们叙述了法国科学家Aspect在80年代初期证实CHSH-Bell不等式的实验。这期间，CHSH那几个美国物理学家又在干些什厶呢？读者应该记得，其中有波士顿大学的西摩尼和他的学生霍恩。霍恩的Ph.D.工作做完後，便四处找工作，求教职。的确，没有哪个科学家是能够不食人间烟火的，任何时候，生存都是第一要素。霍恩还算幸运，他在距离波士顿不远的Stonehill College找到了一个位置。吃饭的问题虽然解决了。但是，霍恩感兴趣的是有关量子力学的实验啊！那个学校既没有像样的实验室，也没有著名的物理学家。头脑灵活的霍恩绞尽脑汁想办法。他看中了麻省理工学院克利夫·沙尔（注∶沙尔後来是1994年的诺贝尔奖得主）的实验室，想到那儿作有关‘中子’的研究。另外，霍恩当然也不能丢掉Stonehill的饭碗，于是，他去MIT实验室找到沙尔，介绍自己之後，半开玩笑地说∶“我可以经常到这儿玩厶？”没想到沙尔神秘地笑了笑，指着实验室一张大桌子，风趣诙谐地给了他一个满意的回答∶“你就在那儿玩吧！”

霍恩这一玩就玩了十年，从1975年到1985年，十年间的许多假期、夏天、每个不上课的星期二，霍恩都来到MIT沙尔的实验室，作他喜爱的物理实验。可贵的是，他在那儿结识了丹尼尔·格林伯格（Daniel M. Greenberg）和塞林格（Anton Zeilinger），之後多年，三人一直保持友谊，密切合作。这样，才有了後来（1993年）以三人姓名第一字母命名的GHZ论文。

塞林格就是我们在上一节中提到过的，奥地利维也纳大学的著名物理学家，量子传态的先驱。而格林伯格又是何许人也，且让我们慢慢道来。

格林伯格1933年出生于纽约的布朗克斯，後来进入著名的布朗克斯科学高中。这所中学的优秀程度，特别是格林伯格所在的那个1950年毕业班，说起来令人乍舌，不得不刮目相看！布朗克斯科学高中可算是孕育物理学家的温床，它的校友录上闪闪夺目地写着7位诺贝尔物理奖得主的大名！其中包括两位格林伯格的同班同学。他们是1979年的诺贝尔物理奖得主∶格拉肖（Sheldon Glashow）和温伯格（Steven Weinberg）。在1950年的毕业班中，还有曾任美国物理学会会长的 Buckley奖获得者Myriam Sarachik，以及另外好几个任教于美国名校的著名物理学家。

从这一届学生後来在物理研究中获得如此辉煌的成就，我们似乎可以想象当初的少年伙伴们醉心于科学的程度。的确，布朗克斯科学高中并不是用考试和分数来束缚学生，而是留给他们一定的共同活动的时间与空间。丰富的课余生活使得学生们的思维有自由翱翔的天地。当年的学生们还自发组织了一个“科学幻想小说俱乐部”。大家 通过幻想的方式，海阔天空地谈论科学。那时的格林伯格也不是等闲之辈， 根据诺贝尔奖得主格拉肖後来的回忆，他就是在学校的食堂里，与格林伯格一起进餐时，从後者那里第一次学到微积分概念的。

回到上世纪70年代末80年代初，格林伯格和塞林格每年都会到MIT克利夫·沙尔的中子实验室去作一段时间的研究工作。他们在那儿认识了经常来实验室‘玩’的霍恩。除了做与中子相关的正常实验之外，对量子理论基础的共同兴趣，把这三个人的学术研究生涯，紧密纠缠在一起。

大概是1985年的某一天，格林伯格坐在霍恩家的厨房里，看着围着炉子忙碌打转的霍恩，莫名其妙地问了一句∶

“你觉得三个粒子纠缠起来会是个什厶样子？”

“三个粒子纠缠？实验室里能得到吗？” 霍恩满脸疑惑地问。

实验物理学家考虑问题毕竟不一样，霍恩首先想到的是实验的可能性。格林伯格告诉他说，在吴健雄-萨科诺夫的正负电子对湮灭实验中，通常是生成两个纠缠的光子对，但也曾经观察到生成了三个互相纠缠光子的情形，恐怕可以由此例提供一个实验方案。

霍恩考虑了一阵，眼神一亮，说∶“我觉得这是一个非常好的研究课题呀。”他鼓励格林伯格花点时间，首先从数学理论上把三粒子纠缠的问题纠缠清楚了再说。

在朋友的鼓励下，格林伯格开始研究三粒子纠缠，并得到了有趣的结果。我们在下一节中再详细介绍。

上一篇∶Aspect实验  返回目录  下一篇∶从纠缠态到qubit