欧拉在研究费马最后猜想时，也提了一个猜想，欧拉猜想还引出了一个“最短的数学论文”……

在数论的历史长河中，有很多著名猜想。有些猜想被证明，有些猜想被证伪，还有些至今没有结论，仍然是未解之谜。费马大定理的证明过程历经了三百多年，最后被解决了。三百多年中也产生和激发了许多别的猜想。

比如欧拉，就在费马最后猜想的启发下，也提了一个“欧拉猜想”，说的是以下方程无正整数解：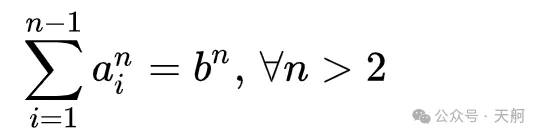

比如说，当n=4时的欧拉猜想，说的是方程：a₁⁴+ a₂⁴+ a₃⁴= b⁴无正整数解。当n=5时的欧拉猜想，说的是方程：a₁⁵+ a₂⁵+ a₃⁵+ a₄⁵= b⁵无正整数解。

欧拉于 1769 年提出这个猜想，一直到欧拉去世，也仍然是个猜想，因为无人证明也无人否定。事实上，持续了将近200 年，也是这个状况。不过后来，现代电子计算机发展起来了，速度越来越快。终于在1966 年，L. J. Lander和T. R. Parkin，在《美国数学学会 公报》上，发表了他们的论文，用两句话推翻了欧拉猜想。

这是当时在严肃的数学期刊上发表的最短数学论文：只有两句简洁的句子：

论文中说，他们利用当时最快的电脑CDC 6600找出了n=5时欧拉猜想的反例：

 1988年，诺姆·埃尔奇斯Noam Elkies找出一个对制造n=4反例的方法。他给出的最小反例如下：

Roger Frye以埃尔奇斯的技巧用电脑直接搜索，找出n=4时最小的反例：

Noam Elkies 还证明了n=4时的方程有无穷多个解。好像现在仍未找到当n> 5时的反例。