1909年,老塞弗里奇在伦敦开了第一家百货商店(Selfridges),以其家族的名字命名。塞弗里奇善于经营有所创新,改变了人们的购物方式,开启了一种新型的商业模式。之后,Selfridges成功地发展成为英国第二大的高档百货连锁店。不过,老塞弗里奇怎么也想不到,50年之后,他的孙子奥利弗·塞弗里奇,用一篇论文,区区十几页纸,就在科学上开辟了一片新天地,成为人工智能中模式识别的奠基人。这篇文章中,我们讲述奥利弗·塞弗里奇的故事。
AI先驱塞弗里奇 奥利弗·塞弗里奇( Oliver Selfridge,1926-2008)出生于伦敦,但他那位创建百货商店的祖父却是出生在美国的威斯康星州。 祖父异常聪明,开始时在芝加哥一家商店工作,很快就成为执行副总裁,然后拥有了一家商店,并将其搬到伦敦,在牛津街开设了塞弗里奇百货公司。 因此,奥利弗的父亲一直拥有美国国籍。在奥利弗十几岁的时候,他随着父母和4个兄弟姐妹,全家搬回到了美国。奥利弗的父亲在美国的Sears Roebuck 公司工作,他对数学一窍不通,但却注意到儿子对数学的兴趣和能力,对奥利弗朝这个方向的发展十分支持,倾注了极大的热情。 像所有聪明好动的男孩子一样,奥利弗小时候不喜欢去学校,但数学成绩表现不凡,他在十三岁时就学习了微积分,达到了大学头两年要求达到的标准。 于是,奥利弗于16 岁顺利地进入麻省理工学院,19 岁本科毕业,主修数学。其间,奥利弗在 17 岁的时候作为一名大三学生加入了海军,因而海军便支付了奥利弗麻省理工学院之后所有的账单。 后来,海军退役后,塞弗里奇留在MIT读研究生,师从诺伯特·维纳(Norbert Wiener)学习数学。他后来参与了达特茅斯会议[图1],是人工智能研究的重要发起人之一。之后继续撰写有关模式识别和机器学习的重要早期论文。 他 1958 年发表的论文“鬼域( Pandemonium )模型:一种学习的范式” [1]被认为是机器智能的经典著作之一。  图1:塞弗里奇,右边照片是在达特茅斯研讨会上,图像来自维基百科 图1:塞弗里奇,右边照片是在达特茅斯研讨会上,图像来自维基百科
塞弗里奇幽默地给他的图像识别模型起了一个新颖的名字:鬼域。Pandemonium一词,取自17世纪英国诗人约翰·弥尔顿1667 年的史诗《失乐园》,意为“所有的恶魔”,或者是地狱之都,简译为“鬼域”,一个喧闹骚动、群魔乱舞的幽灵世界,图1的背景是画家约翰·马丁1841年以鬼域为主题的著名画作之一。 在塞弗里奇的鬼域模型中,将人体大脑及感官中不同的部分,比喻为不同的“鬼怪”,可将它们想象成现代人工神经网络中不同层次的不同神经元组合。这许多鬼怪幽灵在模式识别中扮演着不同的角色,各司其职。后面我们将简单介绍,小鬼们是如何分工合作完成图像识别任务的。 科学江湖高手云集 首先需要回顾一下人类企图模拟自身神经系统的历史,这是塞弗里奇建立鬼域模型的背景。一般认为,这方面最早的工作起始于美国神经生理学教授沃伦·麦卡洛克(Warren McCulloch,1898-1968),[图2c]。1941年,当时已功成名就的沃伦·麦卡洛克,从东部搬到美国芝加哥大学医学院,担任神经生理学教授。到芝加哥后不久,一位朋友介绍他认识了沃尔特·皮茨(Walter Pitts,1923-1969),[图2a]。 皮茨出生于密歇根州底特律一个教育程度不高的家庭,是一个善于自学的神童。他从小就自学逻辑和数学,并精通多种语言,包括希腊语和拉丁语。皮茨 12 岁时,在图书馆呆了三天,阅读英国著名数学家罗素的大作《数学原理》,读后他写信给罗素,指出了他认为第一卷前半部分存在的严重问题。 罗素很感激他,并邀请他在12岁时到剑桥大学学习。但皮茨没有接受这个邀请; 然而,皮茨决定成为一名逻辑学家。 15岁时,他离家求学。  图2:当年MIT的相关人物 图2:当年MIT的相关人物
1938 年秋天,罗素是芝加哥大学的客座教授,15岁的皮茨去参加了罗素的讲座。尽管皮茨没有注册为学生,但他留在那里继续听课,包括罗素的课。在罗素的指导和帮助下,皮茨与多位数学家、逻辑学家、神经解剖科学家等合作工作过,并成为芝加哥大学的博士生。即便如此,皮茨当时却仍然是一个没有收入、无家可归的,芝加哥大学校园中的流浪汉。 1938 年,皮茨遇到了医学预科生杰罗姆·莱特文 (Jerome Lettvin),[图2b]。莱特文1920年出生于芝加哥的一个乌克兰新移民家庭,父亲是律师,母亲是钢琴教师。起初,母亲希望莱特文成为钢琴家,但儿子不感兴趣,因此,父母送学琴不利的杰罗姆去学医。莱特文遇见了皮茨后,年龄相仿的两个年轻人,从此成为亲密的朋友。 皮茨在大学校园里,白天选择喜欢的课程旁听,晚上就随便找个教室睡觉,没有固定的住处。因此,麦卡洛克到芝加哥认识了皮茨和莱特文之后,便邀请皮茨与他的家人住在一起。两人虽然年龄相差悬殊,资历迥异,但却有许多共同的东西将他们连接在一起,而在对神经元模型的思考方面,两人的知识面又能互相弥补。两位科学家都欣赏数学家莱布尼茨, 皮茨熟悉莱布尼茨在计算方面的工作,麦卡洛克考虑,神经系统是否可以被视为莱布尼茨所描述的一种通用计算设备? 那时候的麦卡洛克已经发表了多篇关于神经系统的论文,是该领域有名的专家。而皮茨,虽然才18、9岁,但他已经在数理逻辑领域有所建树,并获得罗素及冯诺依曼等人的赏识。二人都坚信数学模型可以描述、模拟大脑的功能。在这个共同的信念的驱使下,二人于1943年,发表了一篇开创性的神经网络论文“神经活动中内在思想的逻辑演算”[2]。提出了最早的人工神经网络模型:麦卡洛克-皮特斯神经元(McCulloch-Pitts Neuron)模型。该模型旨在用二进制开关的“开”与“关”的机制来模拟神经元的工作原理。在论文中,麦卡洛克与皮特斯证明了该简化模型可以用于实现基础逻辑(如“与”、“或”、“非”)运算。 那么,这几位当年在芝加哥思考和研究“人工神经元”的科学家,又是如何与我们本文介绍的主角:奥利弗·塞弗里奇,关联起来的呢? 那是后来在麻省理工学院的事情。塞弗里奇在二战结束,从海军退役后,便回到了MIT读研究生,师从大名鼎鼎的诺伯特·维纳(Wiener,1894-1964)[图2d]学习数学[3]。 维纳出生于美国,父母都是犹太移民,维纳从小被父母用一种特殊的方式培养成神童,而他也的确是个神童,他18岁就获得了数理逻辑的博士学位。战后,他在麻省理工学院教授数学,以讲课的技巧恶劣而闻名,在课堂上经常心不在焉,闹出不少笑话。二战时,他在枪炮控制方面工作,引发了他对通讯和反馈的兴趣,之后著有《控制论》一书,促成了控制论的诞生。 尽管现在大多数学者并不将控制论归类于人工智能的范畴,但当年维纳心中雄心勃勃的研究计划里,的确是包括了“人类神经系统研究”这种类似的课题的。 因此,麦卡洛克和皮茨发表了第一个神经元模型后,莱特文将好友皮茨介绍给了维纳,维纳也感兴趣。这样,神童顺利地搬到了波士顿,与昔日神童维纳一起工作,成为他的非官方学生。 当年的维纳正在写他的《控制论》,便安排他的学生:皮茨和塞弗里奇,帮助他处理书稿中各个方面的问题。当时的两位年轻人,加上莱特文等,既是同学又兼室友。他们在一起工作、生活、玩耍,都十分开心。特别是对当年还不到20岁,原本学习逻辑的奥利弗·塞弗里奇而言,通过这几位好友,接触了神经网络,了解了理论神经生理学的主题。开始对神经网络可进行的特定处理,以及对“学习”的一般属性都颇感兴趣。计算领域的其他大神,例如冯诺依曼等,也不时拜访MIT,这种环境启发了塞弗里奇跨界思维的科学方法,因而做出了不凡的成绩。 1951年,维纳说服MIT的领导聘请了这几位神经系统生理学家。 麦卡洛克从芝加哥最后搬过来,大家一起成立了一个小组。然而好景不长,1952年,维纳突然反对麦卡洛克,并宣布与这个小组的所有人,包括皮茨、塞弗里奇、莱特文等,断绝一切关系,在他的余生中不再与这些人说话或承认他们的存在。这次重大变故的原因可能来自两方面:维纳的妻子是主要原因,她讨厌麦卡洛克,看不惯他与一伙年轻人的“自由主义”,还对他们编出了一个有关她女儿的莫须有的谎言故事作为罪名。第二个原因,则可能是与维纳本人及其家族严重的精神分裂躁郁症有关[4]。 总之,这次不欢而散,对皮茨这位脆弱的天才造成了致命的打击,因为他当时的生活完全依赖于与维纳的关系,实际上这次事件也不利于维纳 “控制论” 的发展,但这些都是后话,暂且不表。 蛙眼蛙脑跨行思维 作为维纳的博士生,两边“断交”使得塞弗里奇最终没有获得博士学位,他后来加入了MIT的林肯实验室,参与建造第一个扩频系统。1953 年,塞弗里奇在那儿遇到了刚刚从普林斯顿大学毕业的马文·明斯基 (Marvin Minsky,1927-2016),1954 年,又遇到了来自卡内基的心理学家:艾伦·纽厄尔 (Allen Newell,1927-1992),二人都对人工智能极感兴趣。因此,后来便有了1955年在西方联合计算机会议上召开的“真正”第一次人工智能会议,以及再后一年的达特茅斯会议。 1959 年,四位人工神经网络科学家( Humberto Maturana、Lettvin、McCulloch 和 Pitts)发表了一篇著名的论文:“青蛙的眼睛告诉青蛙的大脑什么?”,或简称为“蛙眼”。作者中除了本文上面介绍过的几位之外,还加了马图拉纳(Humberto Maturana,1928-2021),他是一位智利生物学家和哲学家。  图3:“蛙眼”论文[5],1959 图3:“蛙眼”论文[5],1959
“蛙眼”这篇文章对塞弗里奇启发很大。在此之前,人们只知道视网膜上的细胞可以感受简单的、代表光线有无的信息,许多人认为视网膜只是检测个别的像素并将其传送到大脑。而这次的实验数据,最终证明了:不仅仅是生物的大脑处理复杂信息,生物眼睛的图像处理过程中,“眼睛中的模拟过程至少做了部分解释工作”,并不仅仅是“数字的神经元通过其它神经元,完全由大脑使用数学逻辑的精确实现来计算信息”。“蛙眼”论文发表在《Proceedings of the IRE》(现在的《IEEE》)上,因为当时的《神经生理学杂志》不接受它。 该论文对青蛙的部分大脑进行了详细的功能描述,也描述了视觉系统并展示了各种“错误检测器”的视觉特征检测器的存在。实验表明,青蛙眼睛里也有专门用来感受复杂运动的特征感受器。眼睛也能识别特征,不只是简单地感受光线有无。例如,青蛙看见一只虫子嗖的飞过来,蛙眼立刻有反应,将虫子这一特征物体告诉大脑,而它一般对背景的慢变化却无动于衷。据说,当莱特文第一次在会议上公布这个结论时,遭到了同行们无一例外的嘲笑,但是,在之后的10年间,这篇文章成为了引用率最高的科学论文之一。莱特文当年还制造了第一根微电极针,用于读取青蛙视神经中的单个轴突。 因此,塞弗里奇认为,无论是在想法还是实验操作方面,“蛙眼”都是一部绝对出色的作品。 这项工作的结论让塞弗里奇认识到:特征识别异常重要。因此他一直关注类似的课题,在 1955 年的西方联合计算机会议上,他发表了关于模式识别系统的第一篇论文。论文中包括了如何识别正方形的问题,描述了正方形的特征:包括了角和线,并探求如何在嘈杂的背景下检测到“角和线”等等。 塞弗里奇是第一个用足够具体的术语来表达模式识别可以被计算机化的人。 塞弗里奇也意识到以跨学科的方式进行工作的重要性,在那个年代,对这些东西感兴趣的人还不是很多,人工智能才刚刚起步,约翰·麦卡锡等新人不断加入,香农和冯·诺依曼等仍然对此很感兴趣。这些不同行业的科学家们,倾向于互相了解、互相交谈,有意无意地开创了十分有利于科学发展的,跨学科的思维方式。 塞弗里奇几乎与此同步地开发了他的《Pandemonium》鬼域模型,其中融入了他的许多想法,比如并行分布式处理、自适应多层网络、特征检测器等等。 鬼域模型与“蛙眼”两篇论文之间有很多联系,因为塞弗里奇与“蛙眼”作者之间密切合作互相影响。 特征识别鬼域模型 我们以英文字识别为例来解释鬼域模型。当提到图像识别,人们一开始可能自然会思考用比较像素(pixel)的方法,如图4所示。 例如,为了识别图4b接受到的图像是哪一个字母?我们可以将它与计算机中储存的26个英文字母的标准模板相比较。即将图像b分解为若干个像素,每个像素被赋予一个二进制数值(0或1),然后将这一串像素值与26个模板的像素值比较并计算其符合度,如果与某个模板(例如,图4a的L模板)符合度大于某个规定的阈值(例如97%),那么,就可以判定图像是该模板对应的字母(L)。 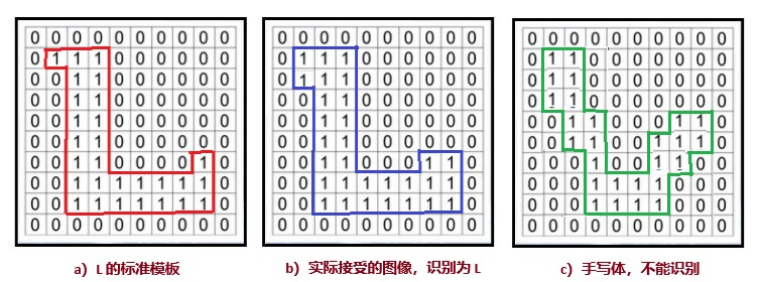 图4:比较像素的图像识别法 图4:比较像素的图像识别法
稍微想一想就能看出上面方法没有多大用处,它无法识别手写的字母,比如图4c那种。 从前面 “蛙眼”文章的介绍中便能体会到,青蛙识别图像的方法,都比图4所示的方法高明多了。也就是说,需要识别的,重点不是每个像素的信息,而是物体的结构特征,这也就是塞弗里奇模型的关键所在。 在塞弗里奇的鬼域模型中有四种幽灵,它们分别是: 1.图像幽灵:守在地狱门口,负责记录和传递输入数据或图像;2.特征幽灵:负责某个特征,例如英语字母中的“横、竖、斜、圈、弧”等等;3.认知幽灵:例如上例中有26个认知幽灵,各负责一个字母;4.决策幽灵:最后确认结果并输出。 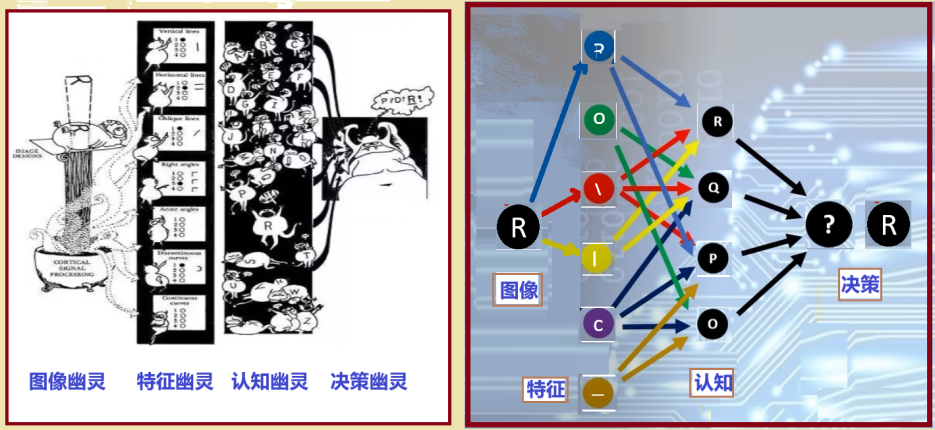 图5:鬼域模型示意图 图5:鬼域模型示意图
图5的左图来自于一本心理学教科书[6],它很形象地描述了鬼域模型中四种幽灵的不同角色。我们用图5右图为例,来解释鬼域模型是如何工作的。 1、首先,图像幽灵接收外来的输入,在我们的例子中,一次接受一个字母,所以,一个图像幽灵守门就可以了。比如图中的输入是字母“R”,图像幽灵将“R”传递到下一阶段的特征幽灵。 2、特征幽灵描述构成英文字母的各种模式特征,因此数目众多,不过图5中只显示了其中的6种,分别用不同颜色的圆形表示。因为输入的是“R”,可以分解为“右半圆、竖、右斜线”3个结构特征。所以,最上面的表示“右半圆” 的蓝色幽灵,检测到了输入包含了它所具有的特征,于是,蓝幽灵大叫一声。同样的,第3个特征“竖”的红幽灵,和第4个特征“右斜线”的黄幽灵,也都分别探测到了输入中有它们,也大叫起来。这3个特征幽灵的叫声,传递给下一阶段的认知幽灵。 3、在我们的例子中,每个认知幽灵代表一个字母,所以应该至少有26个,不过图5中只画出了“R、Q、P、O“4个。认知幽灵探测从特征幽灵那儿传过来的叫声,辨别是由哪些特征幽灵发出来的,与自己代表的字母的特征相比较,计算符合度,并根据符合度大小发出一定音量的声音,符合度越大,音量就越大。在所给的例子中,认知幽灵”R“,发现传来的3个叫声正好完全符合R的3个结构,也就是符合度等于100%,所以,它就发出最大的叫声,而代表其它字母的认知幽灵,例如幽灵”P“,检测到3个叫声中有2个符合,所以符合度等于2/3。然后,它也就只能用2/3的音量来发声了。 4、最后那个决策幽灵的工作比较简单,它只需要根据认知幽灵的声音大小来作决策,选取叫得最响的那个认知幽灵所代表的字母作为输出,任务就完成了。 在这个模型中,各种幽灵都在不停地大叫大嚷,一片喧嚣,鬼哭狼嚎,要不怎么会叫它“鬼域模型”呢。不过,尽管这个名字听起来可怕,但工作原理却不难理解。并且,这个六十多年前就有了的模型,提出了现代机器学习中的许多重要概念,对AI的发展,起到了重要的启发作用。因此,奥利弗·塞弗里奇功不可没。 参考文献: [1]Selfridge, O. (1959) Pandemonium: A Paradigm for Learning, Proceedings of Symposium on the Mechanization of Thought Processes. National Physics Laboratory, Teddington.[2]Warren S. McCulloch and Walter Pitts. A logical calculus of the ideas immanent in nervous activity. Bulletin of mathematical biophysics, vol. 5 (1943), pp. 115–133.[3]An Interview with Oliver Selfridge,January 2008,In book: The Mechanical Mind in History (pp.397-408)Publisher: MIT Press[4] Jim Siegelman 和 Flo Conway (2004),《信息时代的黑暗英雄:寻找诺伯特·维纳—控制论之父》。[5]Lettvin, J.Y; Maturana, H.R.; McCulloch, W.S.; Pitts, W.H., What the Frog's Eye Tells the Frog's Brain Archived 2011-09-28 at the Wayback Machine, Proceedings of the IRE, Vol. 47, No. 11, November 1959[6]Lindsay, P. H., & Norman, D. A. (1972). Human information processing: An introduction to psychology. (本文于3/20/2024首次发布于微信公众号“知识分子”)
|
