戴榕菁 在《弯曲的只是空间。。。》一文中我提到根本找不到爱因斯坦在什么时候说过重力场中的光速是常量,却能找到他在不止一篇文章(【[1],[2]】)中提到不能象在狭义相对论中那样假设光速在重力场为绝对常数,但是现在的教科书中都一律声称光速在重力场中甚至黑洞中都是常数。其实,由Philip Gibbs在1996年撰写Steve Carlip在1997年更新的网络文章【[3]】中就已经指出了这点。 如我在写上文时的状况一样,Philip Gibbs和Steve Carlip他们也没有搞清楚后人出于什么原因替爱因斯坦做出重力场中的光速必须是常数的假设,只是说他们无法想象光速可以不是常数(可见他们的想象力不佳)。 昨天我在贴出《一百多年前的文章出版质量》一文后终于从作为该文链接的爱因斯坦的原文中搞清了后人为什么要替爱因斯坦做出在重力场中的光速也必须是常数的假设的原因-----那是因为爱因斯坦他自己在那篇文章中已经实质性地否认了他作为该文的前提条件所提出的光速在重力场中可以随位置变化这一假设的! 在作为上文的链接的“Outline of a Generalized Theory of Relativity and of a Theory of Gravitation【[4]】”第156页上有这么一句话: First, from the role that ds plays in the law of motion of the material point, we can draw the conclusion that ds must be an absolute invariant (scalar); from this it follows that the quantities guv form a covariant tensor of the second rank,6 which we call the covariant fundamental tensor. 其中的ds由下式给出: 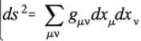
(1)
它对应着狭义相对论中的闵可夫斯基空间的 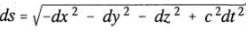
(2)
爱因斯坦所说的“ds must be an absolute invariant”指的应该是在局部的绝对不变量,也就是在任意点的局部,不论在什么坐标系中ds都应该是一样的。但我们知道闵可夫斯基的平坦时空是黎曼时空的一个特例,也就是说在平坦的时空中(1)蜕化为(2)式。所以爱因斯坦所说的ds必须是绝对不变量也必须使得(2)在局部的坐标变换下是绝对的不变式。 但是,我们知道作为闵可夫斯基的时空距离的(2)式在坐标变换下是绝对不变量的前提必须是要满足洛伦兹变换,而洛伦兹变换的前提是光速为常量。 现在爱因斯坦在该文的开头已将光速c定义为可随位置变化的变量,那么为了保证(2)是局部坐标变换下不变量,我们必须要求c在局部为不变的常量。这乍听起来似乎没问题,但实际上与爱因斯坦所提出的c是可以随位置而变的这一条件是相抵触的。这是因为:如果c是可以随位置连续变化的量,那我们一定可以在重力场中画出一组封闭的等c线。在每一点的局部,我假设沿着等c线的光速是常量是没有问题的。但如果我们把沿着等c线的梯度方向,也就是垂直于等c线的方向上的c也假设为常量的话,那就等同于假设光速在整个重力场中是常量,也就是彻底否定了爱因斯坦自己所做的光速在重力场中可以随位置而变化的这一假设。 所以说,实际上是爱因斯坦自己在提出光速在重力场中可以随位置而变化的假设后,在同一篇文章中通过“ds must be an absolute invariant”这一条件又否定了自己的这一假设! 但是,如Philip Gibbs和Steve Carlip在1996年及1997年指出的那样,爱因斯坦生前似乎并没有意识到这个问题,而是后人才将重力场中的光速重新定义为常量的。这似乎意味着在爱因斯坦生前并没有一位够分量的数学家向他指出过这个问题。 这里我们又一次地遇到这样一个令人十分不解的疑问:上述这个“ds must be an absolute invariant”必然导致光速在重力场中不能随位置而变的简单的数学结论怎么会没有被爱因斯坦,庞加莱,洛伦兹,希尔伯特,诺伊德,亚伯拉罕这些与相对论有关的数学大咖注意到??? 我之前已经对于“将单个光源运动引起的Heaviside椭球体的数学公式引申为洛伦兹变换而用到大量粒子构成的宏观物体必然会由于数学难度的增加而违背热力学第二定律”这一简单的数学结论会在过去一百年里没引起包括所有大咖在内的无数数学家的注意表示了困惑不解。 这一次虽然后来的物理学家和数学家们显然已经注意到了“ds must be an absolute invariant”意味着光速必须不变这个问题,但是当初这样一个连中学生都应该注意到的简单的数学问题是怎么会在那样一群精英人精的眼皮底下混过去的???? 实在令人费解。。。。。。 注:以上的讨论并没有涉及到狭义相对论的对错问题。
[[1]] Einstein, A. (1912). “The speed of light and the statics of the gravitational field”. Translated by D. H. Delphenich.“Lichtgeschwindigkeit und Statik des Gravitionsfeldes,” Ann. Phys. (Leipzig) 38 (1912), 355-369. Available at: http://neo-classical-physics.info/uploads/3/4/3/6/34363841/einstein_-_speed_of_light_and_grav.pdf [[2]] Einstein, A. (1916). “Relativity: The Special and General Theory”. Translated by Robert William Lawson. Part II. Available at: https://en.wikisource.org/wiki/Relativity:_The_Special_and_General_Theory/Part_II [[3]] Gibbs, P. (1996). “Is The Speed of Light Constant?”. Retrieved from: https://www.desy.de/user/projects/Physics/Relativity/SpeedOfLight/speed_of_light.html [[4]] Einstein, A. (1913). “Outline of a Generalized Theory of Relativity and of a Theory of Gravitation”. Retrieved from: https://einsteinpapers.press.princeton.edu/vol4-trans/163 (page 151 to 171)
|
