戴榕菁
一年多前,我写了一篇题为“你真能相信他们的实验?”的文章。本文是该文的续篇,因为内容精彩得多,所以在标题后面多加了一个问号。 过去一段时间里,我在将“When Philosophy Is Disparaged”编写为一本书并联系出版社出版之余,因受academia.edu的Didier的影响,一直在关注围绕着μ子衰变的理论问题,主要是那个基本粒子标准模型因受到狭义相对论的影响而出现的与基本概念有关的问题【[1],[2],[3],[4]】。 在阅读所谓测量μ子衰变时间的实验文章时,我发现了一个非常有趣的现象:相对论实验物理学家们居然可以得出逻辑上不可能出现的结果来。。。。 这里先给大家简单地回顾一下狭义相对论的基本核心内容:洛伦兹的动钟变慢和动尺缩短假设: ****** 洛伦兹说运动的坐标系的时间变慢,长度缩短。而这变慢或缩短的比例叫做洛伦兹因子,它由下式表示: γ=1/(1-v2/c2)1/2 (1) 具体地说,根据洛伦兹的假设,在运动坐标系里的时间要除以γ,长度也要除以γ,也就是乘以γ的倒数。 ****** 一个被那些不同的相对论实验物理学家们共同声称且被整个物理学界共同接受了近一个世纪的结论是他们实验中测得的μ子速度的统计平均值,和γ(即静止坐标系与运动坐标系里的时间或长度的比例)的统计评价值可以非常完美地拟合(1) 式给出的结果。。。。但这是不可能的。主要有以下两个原因: 原因一 计算γ的公式(1)是高度非线性的,因此它是不能用线性拟合来进行近似计算的。这里要注意μ子实验的原始数据都是离散性很大的,原因是人们根本不可能精准地控制每个μ子的运动速度。 假设我们有一组速度v的范围由0.1c 到0.9999c的μ子,且通过统计的方法得出它们的平均速度为0.5c。这里c是光速。 对于v=0.1c,我们由(1)得出γ=1.005037815, 对于v=0.9999c,我们由(1)得出γ=70.71244595。 假设我们由实验得出的γ值正好都落在了上面两个γ值的范围之内,即假设实验测得的γ 的范围是从1.005037815 到 70.71244595。再假设通过统计拟合的方法得到γ的平均值为35。 对于v=0.5c 由(1)式我们得到γ=1.154700538, 而对于γ=35 由(1)式我们得到v=0.999591753c。 很显然,1.154700538 ≠ 35, 0.5c≠0.999591753c. 也就是说,我们根本不可能让具有线性拟合性质的统计平均的值来满足高度非线性的计算洛伦兹因子的(1)式! 再次强调一点: μ子实验的原始数据都是离散性很大的,原因是人们根本不可能精准地控制每个μ子的运动速度。 上面的数据是我自己随意选择的,为的是让读者更好地体会高度非线性的(1)式与具有线性特征的统计拟合之间的不一致性。这么说吧,假如我们有100个μ子,每个μ子的速度v和γ值之间都完美地符合(1)式,只要这组μ子的速度具有一定的离散性,那么它们的速度v的统计平均与γ值的统计平均之间就不可能完美地符合(1)式。 下面我们来看一个实际的例子。 上世纪70年代在《自然》杂志刊登的一篇文章【[5]】说,他们测得运动μ子的寿命是64.442微秒,而静止μ子的寿命是2.1948微秒。因此它们的比例(即γ)是64.378/2.1948=29.332。而他们通过测量μ子的速度然后运用(1)式计算出来的γ为29.327。哇,近乎完美! 但问题是上面的64微秒的μ子寿命是从总长600微秒的实验中实测跨度为几百微秒的离散数据中求统计平均得到的, 而它的速度是由下图的原始数据统计得来的:
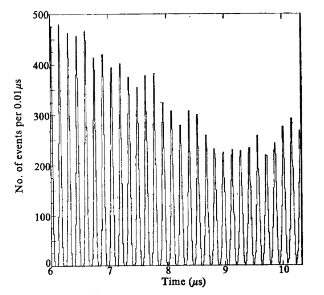
由该图可见其离散度是最小速度几乎达到最大速度的一半。 具有这样离散度的原始数据得出的速度v与γ的统计平均值居然能几乎完美地满足(1)?对此,我不得不问一句:你真的能相信吗?? 原因二 如我之前反复指出过的(参见【[6]】【[7]】),用洛伦兹动钟变慢或动尺缩短解释μ子运动存在着逻辑上混乱:当观察者站在地球上时,他只能用动钟变慢而不能用动尺缩短;当观察者跟着μ子一起运动时,他只能用动尺缩短而不能用动钟变慢。假如他反过来用动钟变慢或动尺缩短进行判断,那么他会得出运动的μ子的寿命不但不延长反而缩短的结论! 。。。。。。 以上两个原因都决定了从实验中运用统计的方法通过测量所谓的μ子寿命来验证洛伦兹动钟变慢或动尺缩短的实验是不可能的! 但令人惊奇的是,相对论实验物理学家们居然就能做到逻辑上根本不可能存在的事情,而且从上世纪40年代就开始这么做了。你说奇怪不奇怪?? 难道相对论实验物理学家们生活在一个与我们有着不同的逻辑法则的平行宇宙中??? 这里看来要对Didier说句对不住。。。。因为他在那篇引起我对μ子问题兴趣的文章【[8]】里还一本正经地分析是否可以通过电磁力学的途径来解释那些声称通过统计方法验证了狭义相对论的实验结果。可惜的是他努力要解释的是根本不可能存在的问题!。。。。不过他的那篇文章也还是有其应有的价值:他对μ子作为不可分的基本粒子的假设提出了质疑。
[[1]]戴榕菁 (2024). 与μ子有关的一个哲学错误 [[2]]戴榕菁 (2024). 关于μ子的两点补充 [[3]]戴榕菁 (2024). 那就再补充两点 [[4]] Dai, R. (2024). Scrutinizing Muons Decay Theory. Retrieved from: https://www.academia.edu/118834607/Scrutinizing_Muons_Decay_Theory [[5]]Bailey, J. et al. (1977). Measurement of relativistic time dilatation for positive and negative muons on a circular orbit. Nature Vol 268, 28 July 1977. Retrived from: https://www.researchgate.net/publication/30398795_Measurements_of_relativistic_time_dilatation_for_positive_and_negative_muons_in_a_circular_orbit [[6]]Dai, R. (2023). Debunk A Few World Famous Experiments. Retrieved from https://www.researchgate.net/publication/375002717_Debunk_A_Few_World_Famous_Experiments [[7]]戴榕菁 (2023). 那几个我讨论过的“验证”相对论的实验 [[8]]Viel, D. (2024). Muons Lifetime Stored in a Circular Ring. Retrieved from: https://www.academia.edu/117382566/Muons_Lifetime_Stored_in_a_Circular_Ring.
|
